题目内容
【题目】如图,矩形纸片ABCD中,AB=4,将纸片折叠,使顶点B落在边AD上的点为E,折痕的一端G点在BC上(BG<GC),另一端F落在矩形的边上,BG=5.
(1)请你在备用图中画出满足条件的图形;
(2)求出AF的长.
【答案】(1)图见解析;(2)AF的长为![]() 或3.
或3.
【解析】
(1)根据折叠的性质和顶点B折叠后的落点可确定另一端F的位置,由此画图即可得;
(2)在图1中,过点G 作![]() 于点M,先根据矩形的性质、折叠的性质得出
于点M,先根据矩形的性质、折叠的性质得出![]() ,
,![]() ,
,![]() ,再利用勾股定理可得EM的长,从而可得AE的长,设
,再利用勾股定理可得EM的长,从而可得AE的长,设![]() ,然后在
,然后在![]() 中,利用勾股定理即可得;在图2中,过点G 作
中,利用勾股定理即可得;在图2中,过点G 作![]() 于点N,先根据线段的和差求出FN的长,再利用勾股定理求出EN的长,从而可得EF的长,然后在
于点N,先根据线段的和差求出FN的长,再利用勾股定理求出EN的长,从而可得EF的长,然后在![]() 中,利用勾股定理即可得.
中,利用勾股定理即可得.
(1)根据折叠的性质和顶点B折叠后的落点,可分以下两种情况:
①当另一端F落在矩形的边AB上时,作图结果如图1所示:
②当另一端F落在矩形的边AD上时,作图结果如图2所示:
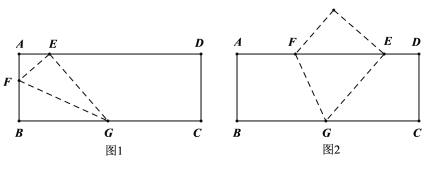
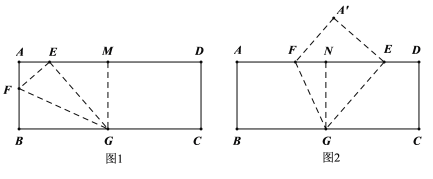
(2)①在图1中,过点G 作![]() 于点M,则四边形ABGM是矩形
于点M,则四边形ABGM是矩形
![]() ,
,![]()
由折叠的性质得:![]() ,
,![]()
在![]() 中,
中,![]()
![]()
![]() 四边形ABCD是矩形
四边形ABCD是矩形
![]()
设![]() ,则
,则![]()
在![]() 中,
中,![]() ,即
,即![]()
解得![]()
②在图2中,过点G 作![]() 于点N,则四边形ABGN是矩形
于点N,则四边形ABGN是矩形
![]() ,
,![]()
由折叠的性质得:![]() ,
,![]() ,
,![]() ,
,![]()
![]()
在![]() 中,
中,![]()
设![]() ,则
,则![]() ,
,![]()
![]()
在![]() 中,
中,![]() ,即
,即![]()
解得![]()
综上,AF的长为![]() 或3.
或3.

 名校课堂系列答案
名校课堂系列答案【题目】某地农民一直保持着冬种油菜的习惯,利用农闲冬种一季油菜.该地农业部门对2017年的油菜籽生产成本、市场价格、种植面积和产量等进行了调查统计,并绘制了如下的统计表与统计图(如图):
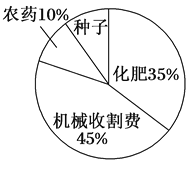
每亩生产成本 | 每亩产量 | 油菜籽市场价格 | 种植面积 |
110元 | 130千克 | 3元/千克 | 500 000亩 |
请根据以上信息解答下列问题:
(1)种植油菜每亩的种子成本是多少元?
(2)农民冬种油菜每亩获利多少元?
(3)2017年该地全县农民冬种油菜的总获利是多少元?(结果用科学记数法表示)