��Ŀ����
ij��װ��˾����һ�ֳɱ�Ϊÿ��50Ԫ��T�������涨����ʱ�����۵��۲����ڳɱ��ۣ��ֲ�����ÿ��70Ԫ�������������� �����������۵���
�����������۵���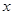 ��Ԫ���Ĺ�ϵ���Խ��ƵĿ���һ�κ�������ͼ����
��Ԫ���Ĺ�ϵ���Խ��ƵĿ���һ�κ�������ͼ����
��1���� ��
��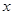 ֮��ĺ�����ϵʽ��
֮��ĺ�����ϵʽ��
��2���蹫˾��õ������������� �����۶�
�����۶� �ܳɱ���Ϊ
�ܳɱ���Ϊ Ԫ����
Ԫ���� ��
��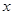 ֮��ĺ�����ϵʽ����д���Ա���
֮��ĺ�����ϵʽ����д���Ա���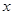 ��ȡֵ��Χ�����������жϣ���
��ȡֵ��Χ�����������жϣ���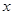 ȡ��ֵʱ��
ȡ��ֵʱ�� ��ֵ������ֵ�Ƕ��٣�
��ֵ������ֵ�Ƕ��٣�
��3������˾Ҫ��֤�����ܵ���4000Ԫ�������۵���x��ȡֵ��ΧΪ����Ԫ���ɽ������κ�����ͼ���𣩣� 
(1) y=-10x+1000��(2) P=-10x2+1500x-50000,6000;(3) 60��x��70.
�������������(1)��֪���㣨60��400���ͣ�70��300�������ô���ϵ�����������y��x�ĺ�����ϵʽ��
��2������������=�����۶�-�ܳɱ������г�P��x֮��ĺ�����ϵʽ���̶���������ֵ��
��3�����������������۵���x��ȡֵ��Χ.
�����������1����y��x�ĺ�����ϵʽΪ��y=kx+b��
�ߺ���ͼ���㣨60��400���ͣ�70��300����
�� �� ���
�� ��� ��
��
��y=-10x+1000��
��2��P="(x-50)(-10x+1000)"
P=-10x2+1500x-50000
�Ա���ȡֵ��Χ��50��x��70��
�� ��
�� ��0��
��0��
�ຯ��P=-10x2+1500x-50000ͼ�����£��Գ�����ֱ��x=75��
��50��x��70����ʱ ��
�� �����������
�����������
�൱x=70ʱ��P���ֵ=6000��
��3����p��4000,��60��x��90,��50��x��70����60��x��70Ԫ.
���㣺1.��һ�κ�����ϵʽ��2.���κ�����Ӧ��.


 ��ͼ���ڵڶ��������ޣ���m��ֵ��
��ͼ���ڵڶ��������ޣ���m��ֵ�� �ڵ�һ�����ڵ�ͼ��ֱ�OA��AB�ڵ�C�͵�D���ҡ�BOD�����S��BOD=4��
�ڵ�һ�����ڵ�ͼ��ֱ�OA��AB�ڵ�C�͵�D���ҡ�BOD�����S��BOD=4��
 .��OΪԭ�㣬������ͼ��ʾ��ƽ��ֱ������ϵ������P1��P2������ֱ��ǣ��C4��9�������C13���C3��.
.��OΪԭ�㣬������ͼ��ʾ��ƽ��ֱ������ϵ������P1��P2������ֱ��ǣ��C4��9�������C13���C3��.
 ֧������ÿ֧5Ԫ�ļ۸�ȫ�����������ӻ��깺���ʻ���ͬʱ������ȥ50Ԫ�����װ���ϣ�
֧������ÿ֧5Ԫ�ļ۸�ȫ�����������ӻ��깺���ʻ���ͬʱ������ȥ50Ԫ�����װ���ϣ�
 �����������ʱ��t��Сʱ���ĺ���ͼ�����Ѳ��ͧԭ�ƻ��㵽���ʱ���� .
�����������ʱ��t��Сʱ���ĺ���ͼ�����Ѳ��ͧԭ�ƻ��㵽���ʱ���� .