题目内容
【题目】阅读材料：人教版八年级上册数学教材第121页的“阅读与思考”内容介绍，在因式分解中有一类形如x2+（p+q）x+pq的多项式，其常数项是两个因数的积，而一次项系数恰好是这两个因数的和，则我们可以把它分解成x2+（p+q）x+pq＝（x+p）（x+q）．
例如，x2+3x+2＝x2+（1+2）x+1×2＝（x+1）（x+2），具体做法是先分解二次项系数，分别写在十字交叉线的左上角和左下角，再分解常数项，分别写在十字交叉线的右上角和右下角：然后交叉相乘，求代数和，使其等于一次项系数（如图），这种方法称为“十字相乘法”．
解决问题：
（1）请模仿上例，运用十字相乘法将多项式x2﹣x﹣6因式分解（画出十字相乘图）
（2）若多项式x2+kx﹣12可以分解成（x+m）（x+n）（m，n为整数）的形式，则m+n的最大值为 ．
【答案】（1）图见解析，x2﹣x﹣6＝（x﹣3）（x+2）；（2）11
【解析】
（1）首先，因式分解是把一个多项式分解成几个整式相乘的形式，然后根据题目中提供的解题思路，分解二次项系数和常数项，分别写在十字交叉线的四个角上，最后交叉相乘求代数和使其等于一次项系数即可．
（2）把﹣12分解为两个整数的积的形式，m+n的值等于这两个整数的和．
（1）画十字相乘图如下：
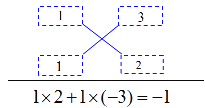
所以x2﹣x﹣6＝（x﹣3）（x+2）
（2）m+n的最大值为 11 ．……………………
﹣12＝1×（﹣12）
＝2×（﹣6）
＝3×（﹣4）
＝4×（﹣3）
＝6×（﹣2）
＝12×（﹣1）
所以，m+n的最大值是12+（﹣1）＝11．
练习册系列答案
快乐小博士巩固与提高系列答案
相关题目
