题目内容
【题目】温润有度,为爱加温.近年来设计精巧、物美价廉的暖风机逐渐成为人们冬天必备的“取暖神器”,今年11月下旬某商场计划购进![]() 、
、![]() 两种型号的暖风机共900台,每台
两种型号的暖风机共900台,每台![]() 型号暖风机售价为600元,每台
型号暖风机售价为600元,每台![]() 型号暖风机售价为900元.
型号暖风机售价为900元.
(1)若要使得![]() 、
、![]() 两种型号暖风机的销售额不低于69万元,则至多购进多少台
两种型号暖风机的销售额不低于69万元,则至多购进多少台![]() 型号暖风机?
型号暖风机?
(2)由于质量超群、品质卓越,11月下旬购进的![]() 、
、![]() 两种型号的暖风机全部售完.该商场在12上旬又购进了
两种型号的暖风机全部售完.该商场在12上旬又购进了![]() 、
、![]() 两种型号的暖风机若干台,并且进行“双12”促销活动,每台
两种型号的暖风机若干台,并且进行“双12”促销活动,每台![]() 型号暖风机的售价比其11月下旬的售价优惠
型号暖风机的售价比其11月下旬的售价优惠![]() ,
,![]() 型号暖风机12月上旬的销售量比其在(1)问条件下的最高购进量增加
型号暖风机12月上旬的销售量比其在(1)问条件下的最高购进量增加![]() ,每台
,每台![]() 型号暖风机的售价比其11月下旬的售价优惠
型号暖风机的售价比其11月下旬的售价优惠![]() ,
,![]() 型号暖风机12月上旬的销售量比其在(1)问条件下的最低购进量增加
型号暖风机12月上旬的销售量比其在(1)问条件下的最低购进量增加![]() ,
,![]() 、
、![]() 两种型号的暖风机在12月上旬的销售额比(1)问中最低销售额增加了
两种型号的暖风机在12月上旬的销售额比(1)问中最低销售额增加了![]() ,求
,求![]() 的值.
的值.
【答案】(1)至少购进![]() 型暖风机400台;(2)
型暖风机400台;(2)![]() 的值为12.5
的值为12.5
【解析】
(1)设购进![]() 型暖风机
型暖风机![]() 台,则B型
台,则B型![]() 台,根据单价乘以数量等于总价,分别表示出两种型号暖风机的总价,建立不等式即可求解;
台,根据单价乘以数量等于总价,分别表示出两种型号暖风机的总价,建立不等式即可求解;
(2)分别表示12月上旬A型、B型暖风机的售价和购进量,并表示12月上旬的销售额,根据比(1)问中最低销售额增加了![]() 建立方程求解.
建立方程求解.
解:(1)设购进![]() 型暖风机
型暖风机![]() 台,则B型
台,则B型![]() 台,由题意得
台,由题意得
![]()
解得:![]()
答:至少购进![]() 型暖风机400台.
型暖风机400台.
(2)由题意得
![]()
令![]() ,化简得:
,化简得:![]()
解得![]() (舍),
(舍),![]() ,即
,即![]()
∴![]() 的值为12.5
的值为12.5

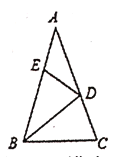
【题目】如图1所示,点E在弦AB所对的优弧上,且![]() 为半圆,C是
为半圆,C是![]() 上的动点,连接CA、CB,已知AB=4cm,设B、C间的距离为xcm,点C到弦AB所在直线的距离为y1cm,A、C两点间的距离为y2cm.
上的动点,连接CA、CB,已知AB=4cm,设B、C间的距离为xcm,点C到弦AB所在直线的距离为y1cm,A、C两点间的距离为y2cm.
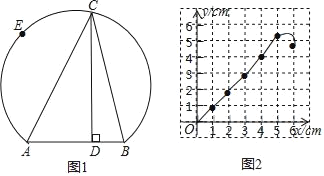
小明根据学习函数的经验,分别对函数y1、y2岁自变量x的变化而变化的规律进行了探究.下面是小明的探究过程,请补充完整.
(1)按照下表中自变量x的值进行取点、画图、测量,分别得到了y1、y2与x的几组对应值:
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y1/cm | 0 | 0.78 | 1.76 | 2.85 | 3.98 | 4.95 | 4.47 |
y2/cm | 4 | 4.69 | 5.26 | 5.96 | 5.94 | 4.47 |
(2)在同一平面直角坐标系xOy中,描出补全后的表中各组数值所对应的点(x,y1),(x,y2),并画出函数y1、y2的图象;
(3)结合函数图象,解决问题:
①连接BE,则BE的长约为 cm.
②当以A、B、C为顶点组成的三角形是直角三角形时,BCspan>的长度约为 cm.