题目内容
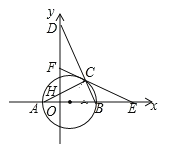
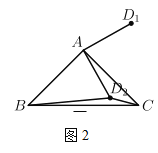
【题目】我们把两条中线互相垂直的三角形称为“中垂三角形”. 如图1,图2,图3中,![]() 是
是![]() 的中线,
的中线,![]() ,垂足为点
,垂足为点![]() ,像
,像![]() 这样的三角形均为“中垂三角形. 设
这样的三角形均为“中垂三角形. 设![]() .
.
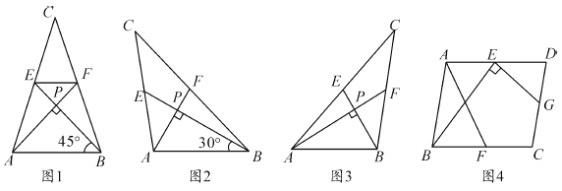
(1)如图1,当![]() 时,则
时,则![]() _________,
_________,![]() __________;
__________;
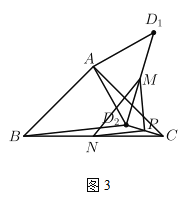
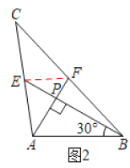
(2)如图2,当![]() 时,则
时,则![]() _________,
_________,![]() __________;
__________;
归纳证明
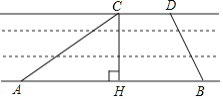
(3)请观察(1)(2)中的计算结果,猜想![]() 三者之间的关系,用等式表示出来,并利用图3证明你发现的关系式;
三者之间的关系,用等式表示出来,并利用图3证明你发现的关系式;
拓展应用
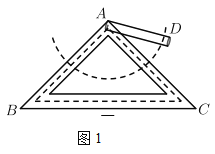
(4)如图4,在![]() 中,
中,![]() 分别是
分别是![]() 的中点,且
的中点,且![]() . 若
. 若![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ,
,![]() ;(3)
;(3)![]() ,证明见解析;(4)
,证明见解析;(4)![]()
【解析】
(1)根据三角形的中位线得出;![]() ,进而得到
,进而得到![]() 计算即可得出答案;
计算即可得出答案;
(2)连接EF,中位线的性质以及![]() 求出AP、BP、EP和FP的长度再根据勾股定理求出AE和BF的长度即可得出答案;
求出AP、BP、EP和FP的长度再根据勾股定理求出AE和BF的长度即可得出答案;
(3)连接EF,根据中位线的性质得出![]() ,根据勾股定理求出AE与AP和EP的关系以及BF与BP和FP的关系,即可得出答案;
,根据勾股定理求出AE与AP和EP的关系以及BF与BP和FP的关系,即可得出答案;
(4)取![]() 的中点
的中点![]() ,连接
,连接![]() ,结合题目求出四边形
,结合题目求出四边形![]() 是平行四边形得出AP=FP即可得到
是平行四边形得出AP=FP即可得到![]() 是“中垂三角形”,根据第三问得出的结论代入,即可得出答案(连接
是“中垂三角形”,根据第三问得出的结论代入,即可得出答案(连接![]() ,交于点
,交于点![]() ,证明
,证明![]() 求得
求得![]() 是
是![]() 的中线,进而得出
的中线,进而得出![]() 是“中垂三角形”,再结合第三问得出的结论计算即可得出答案).
是“中垂三角形”,再结合第三问得出的结论计算即可得出答案).
解:(1)∵![]() 是
是![]() 的中线,∴
的中线,∴![]() 是
是![]() 的中位线,
的中位线,
∴![]() ,且
,且![]() ,易得
,易得![]() .
.
∵![]() ,
,
∴![]() ,∴
,∴![]() .
.
由勾股定理,得![]() ,
,
∴![]() .
.
(2)如图2,连结![]() .
.
∵![]() 是
是![]() 的中线,
的中线,
∴![]() 是
是![]() 的中位线,
的中位线,
∴![]() ,且
,且![]() ,易得
,易得![]() .
.
. ∵![]() ,
,
∴![]() ,
,
∴![]() .
.
由勾股定理,得![]() ,
,
∴![]() .
.
(3)![]() 之间的关系是
之间的关系是![]() .
.
证明如下:如图3,连结![]() .
.

∵![]() 是
是![]() 的中线,
的中线,
∴![]() 是
是![]() 的中位线.
的中位线.
∴![]() ,且
,且![]() ,
,
易得![]() .
.
在![]() 和
和![]() 中,
中,
∵![]() ,
,![]() ,
,
∴ .
.
∴![]() .
.
∴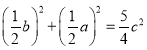 ,
,
即![]() .
.
(4)解法1:设![]() 的交点为
的交点为![]() . 如图4,取
. 如图4,取![]() 的中点
的中点![]() ,连接
,连接![]() .
.
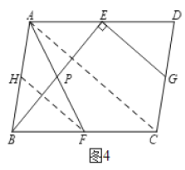
∵![]() 分别是
分别是![]() 的中点,
的中点,![]() 是
是![]() 的中点,
的中点,
∴![]() .
.
又∵![]() ,
,
∴![]() .
.
∵四边形![]() 是平行四边形,
是平行四边形,
∴![]() ,
,
∴![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
∴![]() ,
,
∴![]() 是“中垂三角形”,
是“中垂三角形”,
∴![]() ,即
,即![]() ,
,
解得![]() .
.
(另:连接![]() ,交于点
,交于点![]() ,易得
,易得![]() 是“中垂三角形”,解法类似于解法1,如图5)
是“中垂三角形”,解法类似于解法1,如图5)

解法2:如图6,连接![]() ,延长
,延长![]() 交
交![]() 的延长线于点
的延长线于点![]() .
.
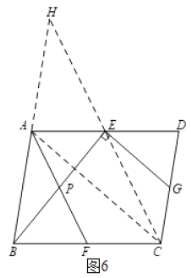
在![]() 中,∵
中,∵![]() 分别是
分别是![]() 的中点,
的中点,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
又∵四边形![]() 为平行四边形,
为平行四边形,
∴![]() ,
,
易得![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 是
是![]() 的中线,
的中线,
∴![]() 是“中垂三角形”,
是“中垂三角形”,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() ,
,
解得![]() .
.
∵![]() 是
是![]() 的中位线,
的中位线,
∴![]() .
.