题目内容
【题目】如图,在![]() 中,
中,![]() ,
,![]() 平分
平分![]() ,若
,若![]() ,
,![]() ,则线段
,则线段![]() 的长为________.
的长为________.
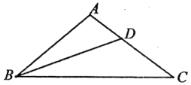
【答案】![]()
【解析】
在BC上取一点E,使BE=AB,作AF⊥BC,连接AN交BD于点G,可证△ABD≌△EBD,根据全等三角形的性质,证得AE=EC,由线段垂直平分线的判定定理可知BD是线段AE的垂直平分线,进而求得BG的长,根据面积相等求得AF的长,再由勾股定理得出EF、AC的长;再等高的三角形的面积比等于底边的比求得CD的长.
解:在BC上取一点E,使BE=AB,作AF⊥BC,连接AN交BD于点G,
∵BD平分∠ABC,
∴∠ABD=∠CBD,BD=BD,AB=BE=6![]()
∴△ABD≌△EBD
∴AD=DE,∠BAE=∠BEA=∠EAD+∠C,
∴∠BAC=∠BAE+∠EAC=∠EAD+∠C+∠EAC=2∠EAC+∠C
又∵∠BAC=3∠C
∴2∠EAC+∠C=3∠C
∴∠EAC=∠C∴AE=EC
∵AB=6![]() ,BC=10
,BC=10![]() ,
,
∴EC=4![]() =AE
=AE
∵AB=BE,AD=DE
∴BD是AE的垂直平分线,
∴AG=2![]()
∴BG=![]()
根据面积相等,得![]() ,即
,即![]()
∴AF=![]()
∴EF=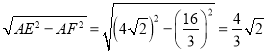
∴CF=CE+EF=4![]() +
+![]() =
=![]()
∴AC=![]()
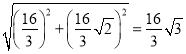
∵S△ADB=S△EDB
∴![]()
∴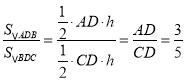
∴![]()

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案
相关题目