Question

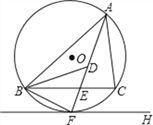
【题目】如图，⊙O是△的外接圆，FH是⊙O的切线，切点为，平分∠．连接交于，连接．（1）求证：FH∥；

（2）若在上存在一点，使得,试说明点是△的内心.

Answer 1

【答案】（1）证明见解析；（2）见解析

【解析】试题分析：

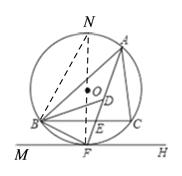
（1）如图，过点F作直径FN，连接BN，由已知易得∠N=∠BAF=∠BFM=∠FAC=∠CBF，就可得BC∥FH；

（2）如图，连接BD，由BF=DF，可得∠DBF=∠BDF，又因为∠DBF=∠DBC+∠CBF，∠BDF=∠BAF+∠ABD，而∠BAF=∠CAF=∠CBF，所以可得∠ABD=∠DBC，即BD平分∠ABC，又AF平分∠BAC，由此可得点D是△ABC角平分线的交点，所以点D是△ABC的内心.

试题解析：

（1）如图，过点作直径，连接.

∴，

∴∠N+∠NFB=900,

∵是⊙O的切线，

∴，

∴,

∴,

∵平分∠，

∴,

又∵,

∴,

∴∥

（2）连接.

∵,

∴,

又∵，

∴，

∴平分，

又∵平分∠，

∴点是△角平分线的交点，

∴点D是△ABC的内心.