题目内容
已知函数y=（k－3）x2＋2x＋1的图像与x轴有交点，则k的取值范围为
A . k < 4 B. k≤ 4 C. k<4且k≠3 D. k≤4且k≠3
A . k < 4 B. k≤ 4 C. k<4且k≠3 D. k≤4且k≠3
B
试题分析：解：（1）当k=3时，函数y=2x+1是一次函数．
∵一次函数y=2x+1与x轴有一个交点，
∴k=3．
（2）当k≠3时，y=（k-3）x2+2x+1是二次函数．
∵二次函数y=（k-3）x2+2x+1的图象与x轴有交点，
∴b2-4ac0．
∵b2-4ac=22-4（k-3）=-4k+16，
∴-4k+16≥0．
∴k≤4且k≠3．
综合（1）（2）可知，k的取值范围是k≤4．
点评：本题考查的是抛物线与x轴的交点及根的判别式，解答此题时要注意分类讨论，不要漏解．
练习册系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
(
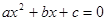≠0)的两根为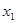
，
，则两根与方程的系数之间有如下关系：
，
.根据该材料完成下列填空：
，
是方程
的两根，则
；
）（
）＝ .
）（
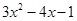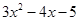）=12的根，则三角形周长只可能为（ ）．
，下列配方正确的是（ ）
；（2）
．
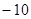，则原方程为