题目内容
【题目】已知：如图，抛物线y=ax2﹣3ax+c(a≠0)与y轴交于点C(0，﹣4)与x轴交于点A．B，点A的坐标为(4，0)．
（1）求该抛物线的解析式．
（2）点D是线段AB上的动点，过点D作DE∥AC，交BC于点E，连接CD．当△CDE的面积最大时，求点D的坐标；
（3）若平行于x轴的动直线l与该抛物线交于点P，与直线AC交于点F，点Q(2，0)．问：是否存在这样的直线l，使得△OQF是等腰三角形？若存在，请求出点P的坐标；若不存在，请说明理由．
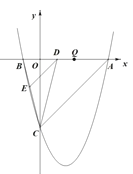
【答案】（1）y=x2-3x-4；（2）
；（3）
，
，
，
【解析】
（1）把点A、C代入抛物线解析式，利用待定系数法求二次函数解析式解答；
（2）设点D坐标为（m，0），过点E作EG⊥x轴于G，令y＝0求出点B的坐标，再表示出BD的长，然后根据△EBD和△BAC相似，利用相似三角形对应高的比等于相似比列式表示出EG，再根据S△CDE＝S△BCDS△BED列式整理即可得解，再根据二次函数的最值问题解答；
（3）分①QO＝QF时，先求出∠OAC＝45°，再根据等边对等角可得∠QFA＝45°，然后求出∠AQF＝90°，从而得到点F的坐标，再根据点P、F的纵坐标相同，利用二次函数解析式求解；②QF＝OF时，过点F作FH⊥x轴于H，根据等腰三角形三线合一的性质可得OH＝
OQ＝1，再求出HF＝AH，然后写出点F的坐标，根据点P、F的纵坐标相同，利用二次函数解析式求解；③OQ＝OF时，先求出点O到AC的距离，根据垂线段最短判断出此时不存在直线l，使△OQF为等腰三角形；
解：（1）把点A(4，0)、C(0，﹣4)代入抛物线解析式y=ax2﹣3ax+c(a≠0)得：
，解得a=1，c=-4，
∴y=x2-3x-4
（2）设点D坐标为（m，0），过点E作EG⊥x轴于G，
当y=0时，x2-3x-4=0，解得：
，
∴B（-1，0），AB=5，
∴BD=m+1，
∵ED∥AC
∴△BDE∽△BAC，
∴
，即
，
∴
，
∵S△CDE＝S△BCDS△BED，
即S△CDE＝
，
∵
，
∴当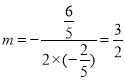
时，△CDE的面积最大，
∴
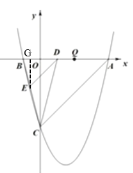
（3）存在，
①当QO=QF时，
∵A（4,0），Q（2,0）
∴AQ=OQ=QF=2，
∵在RT△AOC中，OA=OC=4，
∴∠OAC=45°，
∴∠QFA=∠OAC=45°，
∴∠AQF=90°，
此时F（2，-2）
∵直线l平行于x轴，
∴点P的纵坐标为-2，
∴x2-3x-4=-2，解得：
，
∴，
②当QF=OF时，过点F作FH⊥OA于点H，
由等腰三角形“三线合一”可得：OH=
，
∴AH=4-1=3
在等腰直角三角形AFH中，AH=HF=3，
∴点F（1，-3）
∵直线l平行于x轴，
∴点P纵坐标为-3，
∴x2-3x-4=-3，解得：
∴，
③当OQ=OF时，
∵OA=OC，∠AOC=90°，
∴AC=
，
∴点O到AC的距离为
，
∵OF=OQ=2
，
∴此时，不存在这样的直线l，使得△OQF是等腰三角形，
综上所述，点P的坐标为，，，
