��Ŀ����
����Ŀ����˼���⣩
�Ķ�������龰�Ի���Ȼ�������⣺
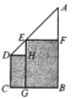
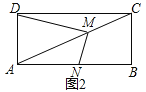
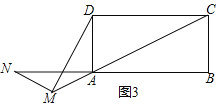
��ʦ�������¶���һ�������Σ�����ƽ���͵��ڵ�����ƽ����2���������ν������������Σ�
С�����ȱ�������һ�������������Σ�
С������ֱ���������Ƿ���������������أ�
��1���ٸ��ݡ����������Ρ��Ķ��壬С��ó����⣺���ȱ�������һ�������������Ρ������ж�С������������Ƿ���ȷ������գ����� �����ȷ������ȷ��������Ҫ˵�����ɣ�
����ij�����ε����߳��ֱ���2��4��![]() ������ABC�������������� ����ǡ����ǡ�������Ҫ˵�����ɣ�
������ABC�������������� ����ǡ����ǡ�������Ҫ˵�����ɣ�
��2����Rt��ABC�У����߳��ֱ���a=5![]() ��c=10������������Ƿ������������Σ���˵�����ɣ�
��c=10������������Ƿ������������Σ���˵�����ɣ�
��3����Rt��ABC�У���C=90����AB=c��AC=b��BC=a����b��a����Rt��ABC�����������Σ���a��b��c��ֵ��
���𰸡���1������ȷ�����ǣ���2����cΪб��ʱ��Rt��ABC�������������Σ���bΪб��ʱ��Rt��ABC�����������Σ���3��a:b:c=![]()
��������
��1���ٸ����������������������εĶ����ж��������٣�
�ڸ����������������������εĶ������ó������
��2����c��б�ߺ�b��б������������ٸ��ݹ��ɶ����жϳ��������������Ƿ�������������εĶ��壻
��3���ȸ��ݹ��ɶ����ó�Rt��ABC����֮��Ĺ�ϵ���ٸ��ݴ������������������ο���a��ʾ��b��c��ֵ�����ɵó������
(1)����ȱ������εı߳�Ϊa��
��![]() ��
��
��ȱ�������һ�������������Σ�
�����ȱ�������һ�������������������������⣻
����ij�����ε����߳��ֱ���2��4��![]() ��
��
�������������εĶ����֪![]() ��
��
�������������������;
(2)�ٵ�cΪб��ʱ��Rt��ABC�������������Σ�
�ڵ�bΪб��ʱ��Rt��ABC�����������Σ��������£�
�����������
�ٵ�cΪб��ʱ, ![]() ��
��
��a=b��
��![]() (��
(��![]() )��
)��
��Rt��ABC��������������.
�ڵ�bΪб��ʱ![]() ��
��
��![]()
��![]()
��![]()
��Rt��ABC������������.
(3)��Rt��ABC��, ![]() ��
��
��c>b>a>0
��![]() ��
��
��Rt��ABC������������
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]()
��a:b:c=![]() .
.

����Ŀ�� ֣���������ѧΪ�˽�ѧ�������Ķ�����ʱ���������Ӹ��꼶ѧ������������һ����ѧ������ͳ�ƣ���������Դ˴�ͳ���������IJ�������Ƶ���ֲ�����Ƶ���ֲ�ֱ��ͼ�������ͼ����Ϣ�ش��������⣺
��� | ʱ��Σ�Сʱ�� | Ƶ�� | Ƶ�� |
1 | 0��x��0.5 | 10 | 0.05 |
2 | 0.5��x��1.0 | 20 | 0.10 |
3 | 1.0��x��1.5 | 80 | b |
4 | 1.5��x��2.0 | a | 0.35 |
5 | 2.0��x��2.5 | 12 | 0.06 |
6 | 2.5��x��3.0 | 8 | 0.04 |
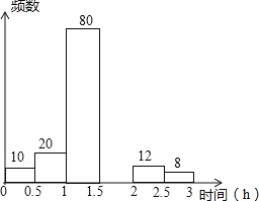
��1������a=______b=______��
��2���벹ȫƵ���ֲ�ֱ��ͼ��
��3�������У�ѧ�����Ķ�����ʱ�����λ�����ڵ�______�飻
��4����У����ѧ��3000�ˣ������ѧ�����Ķ���������1.5Сʱ��������