Question

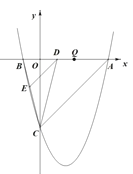
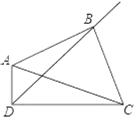
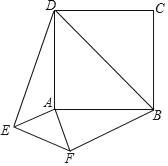
【题目】如图，在边长为3正方形ABCD的外部作Rt△AEF，且AE=AF=1，连接DE，BF，BD，则DE2+BF2=_____．

Answer 1

【答案】20

【解析】

连接BE，DF交于点O，由题意可证△AEB≌△AFD，可得∠AFD=∠AEB，可证∠EOF=90°，由勾股定理可求解．

连接BE，DF交于点O，

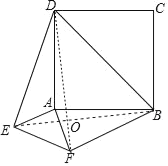
∵四边形ABCD是正方形，

∴AD=AB，∠DAB=90°，

∵△AEF是等腰直角三角形，

∴AE=AF，∠EAF=90°,

∴∠EAB=∠DAF，

在△AEB和△AFD中,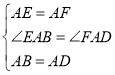

∴△AEB≌△AFD（SAS），

∴∠AFD=∠AEB，

∵∠AEF+∠AFE=90°=∠AEB+∠BEF+∠AFE=∠BEF+∠AFE+∠AFD=∠BEF+∠EFD=90°，

∴∠EOF=90°，

∴EO2+FO2=EF2，DO2+BO2=DB2，EO2+DO2=DE2，OF2+BO2=BF2，

∴DE2+BF2=EF2+DB2=2AE2+2AD2=20，

故答案为：20．