题目内容
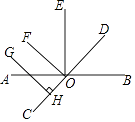
【题目】如图,∠1=∠2.∠GFA=55°,∠ACB=75°,AQ平分∠FAC,AH∥BD,求∠HAQ的度数. 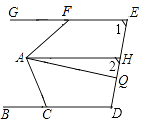
【答案】解:∵∠1=∠2, ∴GE∥AH,
又∵AH∥BD,
∴GE∥BD,
∴∠GFA=∠FAH=55°,∠ACB=∠CAH=75°,
∴∠FAC=55°+75°=130°,
∵AQ平分∠FAC,
∴∠CAQ= ![]() ∠CAF=65°,
∠CAF=65°,
∴∠HAQ=∠CAH﹣∠CAQ=75°﹣65°=10°
【解析】先根据∠1=∠2,判定GE∥AH,进而得到GE∥BD,即可得出∠GFA=∠FAH=55°,∠ACB=∠CAH=75°,进而得出∠FAC=55°+75°=130°,根据AQ平分∠FAC,可得∠CAQ= ![]() ∠CAF=65°,即可得出∠HAQ=∠CAH﹣∠CAQ=10°.
∠CAF=65°,即可得出∠HAQ=∠CAH﹣∠CAQ=10°.
【考点精析】掌握角的平分线和平行线的性质是解答本题的根本,需要知道从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线;两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补.

练习册系列答案
相关题目