Question

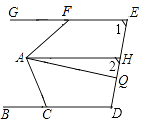
【题目】如图，CD∥AB，∠DCB=70°，∠CBF=20°，∠EFB=130°，问直线EF与AB有怎样的位置关系？为什么？

Answer 1

【答案】解：平行． 证明：∵CD∥AB，
∴∠ABC=∠DCB=70°；
又∵∠CBF=20°，
∴∠ABF=∠ABC﹣∠CBF=70°﹣20°=50°；
∴∠ABF+∠EFB=50°+130°=180°；
∴EF∥AB（同旁内角互补，两直线平行）
【解析】两直线的位置关系有两种：平行和相交，根据图形可以猜想两直线平行，然后根据条件探求平行的判定条件．
【考点精析】根据题目的已知条件，利用平行线的判定与性质的相关知识可以得到问题的答案，需要掌握由角的相等或互补（数量关系）的条件，得到两条直线平行（位置关系）这是平行线的判定；由平行线（位置关系）得到有关角相等或互补（数量关系）的结论是平行线的性质．