题目内容
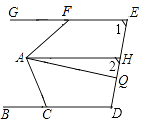
【题目】如图,等腰Rt△ABC中,∠C=90°,D为AC上一点,连接BD,将线段BD绕点D顺时针旋转90°得到线段DE,DE与AB相交于点F,过点D作DG⊥AB,垂足为点G.若EF=5,CD=2![]() ,则△BDG的面积为 .
,则△BDG的面积为 .
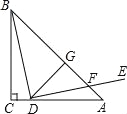
【答案】96
【解析】
试题分析:过点E作EH⊥AC,垂足为H,连接AE.

∵∠BDE=90°,
∴∠BDC+∠EDH=90°.
又∵∠CBD+∠CDB=90°,
∴∠CBD=∠EDH.
在△BCD和△DHE中,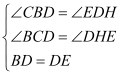 ,
,
∴△BCD≌△DHE.
∴BC=DH,CD=EH=2![]() .
.
∵△ABC为等腰直角三角形,
∴BC=CA.
∴AC=DH.
∴DC=AH=2![]() .
.
∴AH=EH=2![]() .
.
∴AE=![]() =4.
=4.
∵∠BAC=45°,∠EAH=45°,
∴∠FAE=90°.
∴AF=![]() =3.
=3.
∵∠BDF=∠FAE,∠BFD=∠EFA,
∴△BDF∽△EFA.
∴![]() .
.
设DF=x,则BD=DE=x+5.
∴![]() .
.
解得:x=15.
∴DF=15,BD=20.
∴BG=![]() BD=16,DG=
BD=16,DG=![]() =12.
=12.
∴![]() =96.
=96.
故答案为;96.

练习册系列答案
相关题目