题目内容
【题目】如图,直线AB,CD相交于点O,OD平分∠EOB,OF平分∠AOE,GH⊥CD,垂足为H,求证:GH∥FO. 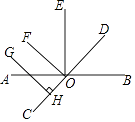
【答案】证明:∵OD平分∠EOB, ∴∠DOE= ![]() BOE,
BOE,
∵OF平分∠AOE,
∴∠EOF= ![]() AOE,
AOE,
∴∠FOD=∠DOE+∠EOF= ![]() (∠AOE+∠BOE)=90°,
(∠AOE+∠BOE)=90°,
∵GH⊥CD,
∴∠GHO=90°,
∴∠GHO=∠FOD,
∴GH∥FO
【解析】根据角平分线的定义得到∠DOE= ![]() BOE,∠EOF=
BOE,∠EOF= ![]() AOE,根据垂直的定义得到∠GHO=∠FOD,根据平行线的判定定理即可得到结论.
AOE,根据垂直的定义得到∠GHO=∠FOD,根据平行线的判定定理即可得到结论.
【考点精析】解答此题的关键在于理解平行线的判定的相关知识,掌握同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行.

练习册系列答案
相关题目