题目内容
【题目】已知抛物线![]() 的对称轴是直线
的对称轴是直线![]() ,与x轴相交于A,B两点(点B在点A右侧),与y轴交于点C.
,与x轴相交于A,B两点(点B在点A右侧),与y轴交于点C.
(1)求抛物线的解析式和A,B两点的坐标;
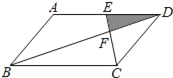
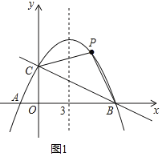
(2)如图1,若点P是抛物线上B,C两点之间的一个动点(不与B,C重合),是否存在点P,使四边形PBOC的面积最大?若存在,求点P的坐标及四边形PBOC面积的最大值;若不存在,请说明理由;
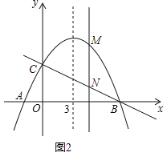
(3)如图2,若点M是抛物线上任意一点,过点M作y轴的平行线,交直线BC于点N,当MN=3时,求点M的坐标.
【答案】(1)抛物线的解析式为![]() ;点
;点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() .(2)存在,点
.(2)存在,点![]() 的坐标为
的坐标为![]() ,四边形
,四边形![]() 的面积的最大值为32.(3)点
的面积的最大值为32.(3)点![]() 的坐标为
的坐标为![]() ,
,![]() ,
,![]() 或
或![]() .
.
【解析】
(1)由抛物线的对称轴为直线x=3,利用二次函数的性质即可求出a值,进而可得出抛物线的解析式,再利用二次函数图象上点的坐标特征,即可求出点A、B的坐标;
(2)利用二次函数图象上点的坐标特征可求出点C的坐标,由点B、C的坐标,利用待定系数法即可求出直线BC的解析式,假设存在,设点P的坐标为(x,![]() ),过点P作PD//y轴,交直线BC于点D,则点D的坐标为(x,
),过点P作PD//y轴,交直线BC于点D,则点D的坐标为(x,![]() ),PD=
),PD=![]() ,利用三角形的面积公式即可得出三角形PBC的面积关于x的函数关系式,再利用二次函数的性质即可解决最值问题;
,利用三角形的面积公式即可得出三角形PBC的面积关于x的函数关系式,再利用二次函数的性质即可解决最值问题;
(3)设点M的坐标为(m,![]() ),则点N的坐标为(m,
),则点N的坐标为(m,![]() ),进而可得出MN=|
),进而可得出MN=|![]() |,结合MN=3即可得出关于m的含绝对值符号的一元二次方程,解之即可得出结论.
|,结合MN=3即可得出关于m的含绝对值符号的一元二次方程,解之即可得出结论.
(1)∵抛物线的对称轴是直线![]() ,
,
∴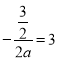 ,解得
,解得![]() ,
,
∴抛物线的解析式为![]() .
.
当![]() 时,
时,![]() ,解得
,解得![]() ,
,![]() ,
,
∴点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.
答:抛物线的解析式为![]() ;点
;点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.
(2)当![]() 时,
时,![]() ,
,
∴点![]() 的坐标为
的坐标为![]() .
.
设直线![]() 的解析式为
的解析式为![]() ,
,
将![]() ,
,![]() 代入
代入![]() 得
得![]() 解得
解得
∴直线![]() 的解析式为
的解析式为![]() .
.
假设存在点![]() ,使四边形
,使四边形![]() 的面积最大,
的面积最大,
设点![]() 的坐标为
的坐标为![]() ,
,
如下图所示,过点![]() 作
作![]() 轴,交直线
轴,交直线![]() 于点
于点![]() ,
,

则点![]() 的坐标为
的坐标为![]() ,
,
则![]() ,
,
∴![]()
![]()
![]()
![]()
![]() ,
,
∴当![]() 时,四边形
时,四边形![]() 的面积最大,最大值是32.
的面积最大,最大值是32.
∵![]() ,
,
∴存在点![]() ,使得四边形
,使得四边形![]() 的面积最大.
的面积最大.
答:存在点![]() ,使得四边形
,使得四边形![]() 的面积最大;
的面积最大;
点![]() 的坐标为
的坐标为![]() ,四边形
,四边形![]() 的面积的最大值为32.-
的面积的最大值为32.-
(3)设点![]() 的坐标为
的坐标为![]() ,则点N的坐标为
,则点N的坐标为![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴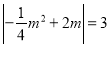 ,
,
当![]() 时,
时,![]() ,解得
,解得![]() ,
,![]() ,
,
∴点![]() 的坐标为
的坐标为![]() 或
或![]() ;
;
当![]() 或
或![]() 时,
时,![]() ,解得
,解得![]() ,
,![]()
![]() ,
,
∴点![]() 的坐标为
的坐标为![]() 或
或![]() .
.
答:点![]() 的坐标为
的坐标为![]() ,
,![]() ,
,![]() 或
或![]() .
.

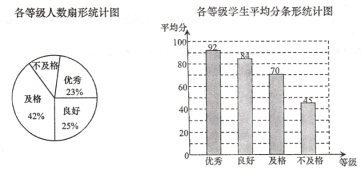
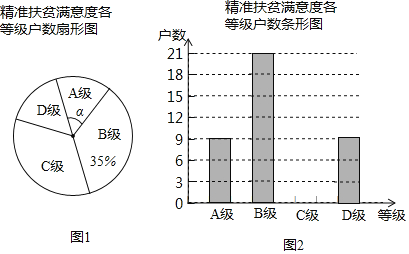
【题目】学校数学社团的同学们在学生中开展“了解校训意义”的调查活动.采取随机抽样的方式进行问卷调查.问卷调查的结果分为![]() 、
、![]() 、
、![]() 、
、![]() 四类.
四类.![]() 类表示非常了解;
类表示非常了解;![]() 类表示比较了解;
类表示比较了解;![]() 类表示基本了解;
类表示基本了解;![]() 类表示不太了解.(要求每位同学必须选并且只能选择一项)统计数据整理如表:
类表示不太了解.(要求每位同学必须选并且只能选择一项)统计数据整理如表:
类别 | 频数 | 频率 |
| 20 |
|
|
| 0.3 |
| 11 | 0.22 |
| 4 | 0.08 |

(1)表中![]() __________;
__________;![]() _________.
_________.
(2)根据表中数据,求出![]() 类同学数所对应的扇形圆心角为_________度.
类同学数所对应的扇形圆心角为_________度.
(3)根据调查结果,请你估计该校1500名学生中对校训“非常了解”的人数;
(4)学校在开展了解校训意义活动中,需要从![]() 类的甲、乙、丙、丁四名同学中随机选取2人参加展示活动,求恰好选中甲乙两人的概率?(请用列表法或是树状图表示)
类的甲、乙、丙、丁四名同学中随机选取2人参加展示活动,求恰好选中甲乙两人的概率?(请用列表法或是树状图表示)
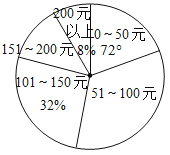
【题目】某社区踊跃为“抗击肺炎”捐款,根据捐款情况(捐款数为正数)制作以下统计图表,但工作人员不小心把墨水滴在统计表上,部分数据看不清楚.
(1)共有多少人捐款?
(2)如果捐款0~50元的人数在扇形统计图中所占的圆心角为72°,那么捐款51~100元的有多少人?
捐款 | 人数 |
0~50元 | |
51~100元 | |
101~150元 | |
151~200元 | 6 |
200元以上 | 4 |