��Ŀ����
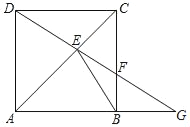
����Ŀ����ͼ��������ABCD�У�AD��BC����C=90�㣬DC=5����CDΪ�뾶�ġ�C����ABΪ�뾶�ġ�B�ཻ�ڵ�E��F���ҵ�E��BD�ϣ�����EF��BC�ڵ�G��
��1����BC���C�ཻ�ڵ�M����BM=ADʱ�����B�İ뾶��
��2����BC=x��EF=y����y����x�ĺ�����ϵʽ����д�����Ķ�����
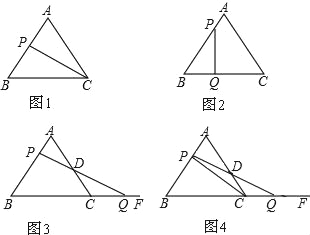
��3����BC=10ʱ����PΪƽ����һ�㣬����P���C�ཻ�ڵ�D��E������A��E��P��DΪ������ı��������Σ���ֱ��д����P�����������������У�

���𰸡���1��![]() ����2��
����2��![]() ����3����
����3����![]() ������29��8
������29��8![]() ����
����
�ۡ�P�����Ϊ![]() ��
��
����������������1���������DM�ij�����֤���ı���ABMD��ƽ���ı��μ��ɽ�����⣻
��2����ͼ2�У�����C��CH��BD������Ϊ��H��������x��ʾBE�ij����ٸ���EG��BEsin��DBC��![]() ����⼴�ɣ�
����⼴�ɣ�
��3�����������ηֱ���⼴�ɽ�����⣻
��⣺��1����ͼ1�У�����DM��
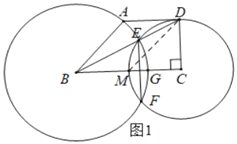
��Rt��DCM��![]() ��
��
��AD��BC BM=AD��
���ı���ABMDΪƽ���ı��Σ�
��AB=DM=![]() ��
��
����B�İ뾶Ϊ![]() ��
��
��2����ͼ2�У�����C��CH��BD������Ϊ��H��
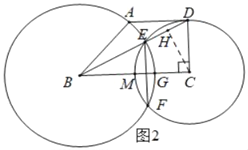
��Rt��BCD��![]() ��
��
��![]() ��
��
�ɵá�DCH=��DBC��
��![]() ��
��
��Rt��DCH��DH=DC![]() sin��DCH=
sin��DCH=![]() ��
��
��CH��BD��
��DE=2DH=![]() ��
��
��![]()
�ߡ�C���B�ཻ�ڵ�E��F��
��EF=2EG��BC��EF��
��Rt��EBG��
![]() ��
��
��![]() (x>
(x>![]() )��
)��
��3������ͼ3�У���PE��ADʱ����PC��DE��H����CH��ֱƽ���߶�DE��
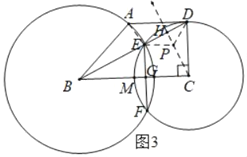
��Rt��BCD��BD=![]() ��CH=
��CH=![]() ��
��
DH=![]() ��
��
��EH=DH=![]() ��
��
��AD��BC��PE��AD��
��PE��BC��
���HEP=��HBC��
��cos��HEP=cos��CBD��
��![]() ��
��
��![]() ��
��
��PE=![]() ��
��
���P�����Ϊ![]() �У�
�У�
����ͼ4�У���AP��DEʱ����AT��BC��T����AD��PC��Q��BD��PC��H��
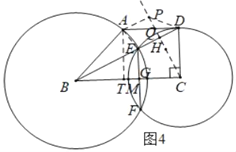
�ɢٿ�֪��DE=2![]() ��BE=BA=3
��BE=BA=3![]() ��AT=CD=5��
��AT=CD=5��
��Rt��ABT��BT=![]() ��
��
��AD=CT=10��2![]() ��
��
����DQH�ס�BDC���ɵ�DQ=![]() ��QH=
��QH=![]() ��
��
��AQ=AD��DQ=![]() ��2
��2![]() ��
��
����APQ�ס�DHQ���ɵ�PQ=![]() ��2��
��2��
��Rt��PDH��PD2=DH2+PH2=29��8![]() ��
��
���P�����Ϊ��29��8![]() ���У�
����
����ͼ5�У���DP��AEʱ����AR��BD��R��
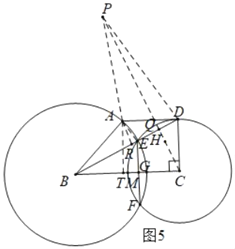
����ADR�ס�DBC��
��![]() ��
��
��AR=2![]() ��2��DR=4
��2��DR=4![]() ��4��
��4��
��ER=DR��DE=2![]() ��4��
��4��
��Rt��ARE��AE=![]() ��
��
��AE��DP��
���AER=��PDQ��
��cos��AER=cos��PDH��
��![]() ��
��
��PD=![]() ��
��
���P�����Ϊ![]() ��
��