题目内容
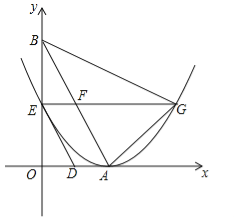
【题目】如图，抛物线
经过点A（﹣3，0），点C（0，4），作CD∥x轴交抛物线于点D，作DE⊥x轴，垂足为E，动点M从点E出发在线段EA上以每秒2个单位长度的速度向点A运动，同时动点N从点A出发在线段AC上以每秒1个单位长度的速度向点C运动，当一个点到达终点时，另一个点也随之停止运动，设运动时间为t秒．
（1）求抛物线的解析式；
（2）设△DMN的面积为S，求S与t的函数关系式；
（3）①当MN∥DE时，直接写出t的值；
②在点M和点N运动过程中，是否存在某一时刻，使MN⊥AD？若存在，直接写出此时t的值；若不存在，请说明理由．
【答案】（1）
；（2）S=
（0＜t≤3）；（3）①t=
；②t=
．
【解析】（1）∵抛物线
经过点A（﹣3，0），点C（0，4），∴
，解得：
，即抛物线的解析式为：；
（2）作NH⊥AM于点H，如由图1所示，∵=
，∴对称轴x=
，∵点A（﹣3，0），点C（0，4），CD∥x轴交抛物线于点D，DE⊥x轴，垂足为E，∴点D（3，4），点E（3，0），OA=3，OC=4，∴AC=5，AE=6，CD=3，∵NH⊥AM，AN=tME=2t，∴△ANH∽△ACO，AM=6﹣2t，∴
，即
，得NH=0.8t，∴S=S梯形AECD﹣S△AMN﹣S△DME﹣S△CDN
=
（3+6）×4-×（6-2t）×0.8t-×2t×4-×3×（4-0.8t）
=，即S与t的函数关系式是S=（0＜t≤3）；
（3）①当MN∥DE时，t的值是，理由：如右图2所示
∵MN∥DE，AE=6，AC=5，AO=3，∴AM=6﹣2t，AN=t，△AMN∽△AOC，∴
，即
，解得，t=；
②存在某一时刻，使MN⊥AD，此时t的值是，理由：如右图3所示，设过点A（﹣3，0），C（0，4）的直线的解析式为y=kx+b，则：
，得：
，即直线AC的解析式为
，∵NH=0.8t，∴点N的纵坐标为0.8t，将y=0.8t代入，得x=0.6t﹣3，∴点N（0.6t﹣3，0.8t）
∵点E（3，0），ME=2t，∴点M（3﹣2t，0），∵点A（﹣3，0），点D（3，4），点M（3﹣2t，0），点N（0.6t﹣3，0.8t），AD⊥MN，∴
，解得：t=．
