题目内容
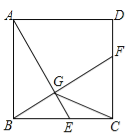
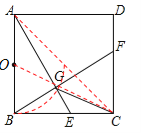
【题目】如图,已知正方形ABCD的边长为2,E是边BC上的动点,BF⊥AE交CD于点F,垂足为G,连结CG.下列说法:①AG>GE;②AE=BF;③点G运动的路径长为π;④CG的最小值为![]() .其中正确的说法是 .(把你认为正确的说法的序号都填上)
.其中正确的说法是 .(把你认为正确的说法的序号都填上)
【答案】②④.
【解析】
试题分析:∵在正方形ABCD中,AE、BD垂直平分,∴当E移动到与C重合时,AG=GE,故①错误;
∵BF⊥AE,∴∠AEB+∠CBF=90°,∵∠AEB+∠BAE=90°,∴∠BAE=∠CBF,在△ABE和△BCF中,∵∠BAE=∠CBF,∠ABE=∠BCF=90°,AB=BC,∴△ABE≌△BCF(AAS),∴故②正确;
根据题意,G点的轨迹是以AB中点O为圆心,AO为半径的圆弧,∴圆弧BD的长=![]() =
=![]() ,故③错误;
,故③错误;
由于OC和OG的长度是一定的,因此当O、G、C在同一条直线上时,CG取最小值,OC=![]() =
=![]() =
=![]() ,CG的最小值为OC﹣OG=
,CG的最小值为OC﹣OG=![]() ,故④正确;
,故④正确;
综上所述,正确的结论有②④.故答案为:②④.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目