Question

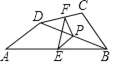
【题目】如图，在四边形ABCD中，点P是对角线BD的中点，点E、F分别是AB、CD的中点，AD＝BC，且∠A+∠ABC＝90°，则∠PEF＝_____．

Answer 1

【答案】45°．

【解析】

根据三角形中位线定理得到PE=AD，∠PEB=∠A，PF=BC，∠DPF=∠DBC，得到PE=PF，∠EPF=90°，根据等腰三角形的性质、三角形内角和定理计算，得到答案．

解：∵AE＝EB，DP＝PB，

∴PE＝AD，∠PEB＝∠A，

∵DF＝FC，DP＝PB，

∴PF＝BC，∠DPF＝∠DBC，

∵AD＝BC，

∴PE＝PF，

∵∠A+∠ABC＝90°，

∴∠EPF＝∠PEB+∠ABD+∠DPF＝∠A+∠ABD+∠DBC＝90°，

∴∠PEF＝∠PFE＝45°，

故答案为：45°．