题目内容
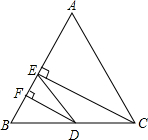
如图，已知△ABC中，BD是∠ABC的角平分线，DE∥BC，交AB于E，∠A=60°，∠C=80°，求：△BDE各内角的度数．
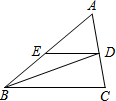
在△ABC中，
∵∠A=60°，∠C=80°，
∴∠ABC=180°-∠A-∠C-=40°，
∵BD是∠ABC的角平分线，
∴∠EBD=
∠ABC=20°，
∵DE∥BC，
∴∠EDB=∠DBC=20°，
则∠BED=180°-∠EBD-∠EDB=180°-20°-20°=140°．
故△BDE各内角的度数为：∠EBD=20°，∠EDB=20°，∠BED=140°．
∵∠A=60°，∠C=80°，
∴∠ABC=180°-∠A-∠C-=40°，
∵BD是∠ABC的角平分线，
∴∠EBD=
| 1 |
| 2 |
∵DE∥BC，
∴∠EDB=∠DBC=20°，
则∠BED=180°-∠EBD-∠EDB=180°-20°-20°=140°．
故△BDE各内角的度数为：∠EBD=20°，∠EDB=20°，∠BED=140°．
练习册系列答案
名校课堂系列答案
相关题目
