题目内容
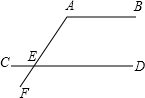
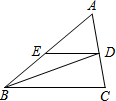
如图，在△ABC中，CE⊥AB于E，DF⊥AB于F，AC∥ED，CE是∠ACB的平分线，试比较∠EDF与∠BDF的大小，并说明理由．
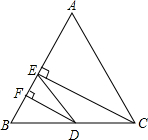
∠EDF=∠BDF．
∵CE⊥AB于E，DF⊥AB于F
∴DF∥CE （垂直于同一条直线的两直线平行），
∴∠BDF=∠BCE （两直线平行，同位角相等），∠FDE=∠DEC （两直线平行，内错角相等）
又∵AC∥ED，
∴∠DEC=∠ACE （两直线平行，内错角相等），
∵CE是∠ACB的角平分线，
∴∠ACE=∠ECB（角平分线的定义），
∴∠EDF=∠BDF（等量代换）．
∵CE⊥AB于E，DF⊥AB于F
∴DF∥CE （垂直于同一条直线的两直线平行），
∴∠BDF=∠BCE （两直线平行，同位角相等），∠FDE=∠DEC （两直线平行，内错角相等）
又∵AC∥ED，
∴∠DEC=∠ACE （两直线平行，内错角相等），
∵CE是∠ACB的角平分线，
∴∠ACE=∠ECB（角平分线的定义），
∴∠EDF=∠BDF（等量代换）．
练习册系列答案
同步奥数系列答案
相关题目
