题目内容
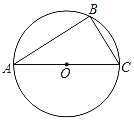
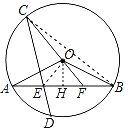
【题目】在圆O中,弦AB与CD相交于点E,且弧AC与弧BD相等.点D在劣弧AB上,联结CO并延长交线段AB于点F,联结OA、OB.当OA=![]() ,且tan∠OAB=
,且tan∠OAB=![]() .
.
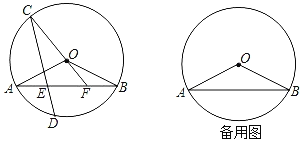
(1)求弦CD的长;
(2)如果△AOF是直角三角形,求线段EF的长;
(3)如果S△CEF=4S△BOF,求线段AF的长.
【答案】(1)4;(2)![]() 或
或![]() ;(3)2+
;(3)2+![]()
【解析】
(1)如图,过点O作OH⊥AB于点H,由锐角三角函数可求OH=1,AH=2,由垂径定理可得AB=4,即可求CD=4
(2)分两种情况讨论,由相似三角形的性质可求解;
(3)先利用面积关系得出![]() ,进而利用△OAF∽△EFC得出比例式,即可得出结论.
,进而利用△OAF∽△EFC得出比例式,即可得出结论.
解:(1)如图,过点O作OH⊥AB于点H,
∵tan∠OAB=![]() ,
,
∴设OH=a,AH=2a,
∵AO2=OH2+AH2=5,
∴a=1,
∴OH=1,AH=2,
∵OH⊥AB,
∴AB=2AH=4,
∵弧AC=弧BD
∴![]() ,
,
∴AB=CD=4;
(2)∵OA=OB,
∴∠OAF=∠OBA,
∴∠OAF=∠ECF,
①当∠AFO=90°时,
∵OA=![]() ,tan∠OBA=
,tan∠OBA=![]() ,
,
∴OC=OA=![]() ,OF=1,AB=4,
,OF=1,AB=4,
∴EF=CFtan∠ECF=CFtan∠OBA=![]() ;
;
②当∠AOF=90°时,
∵OA=OB,
∴∠OAF=∠OBA,
∴tan∠OAF=tan∠OBA=![]() ,
,
∵OA=![]() ,
,
∴OF=OAtan∠OAF=![]() ,
,
∴AF=![]() ,
,
∵∠OAF=∠OBA=∠ECF,∠OFA=∠EFC,
∴△OFA∽△EFC,
∴![]() ,
,
∴EF=![]() ,
,
即:EF=![]() 或
或![]() ;
;
(3)如图,连接OE,
∵∠ECB=∠EBC,
∴CE=EB,
∵OE=OE,OB=OC,
∴△OEC≌△OEB,
∴S△OEC=S△OEB,
∵S△CEF=4S△BOF,
∴S△CEO+S△EOF=4(S△BOE﹣S△EOF),
∴![]() ,
,
∴![]() ,
,
∴FO=![]() ,
,
∵△OFA∽△EFC,
∴![]() ,
,
∴BF=BE﹣EF=CE﹣EF=![]() EF,
EF,
∴AF=AB﹣BF=4﹣![]() EF,
EF,
∵△OAF∽△EFC,
∴![]() ,
,
∴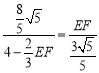 ,
,
∴EF=3﹣![]() ,
,
∴AF=4﹣![]() EF=2+
EF=2+![]() .
.

 中考解读考点精练系列答案
中考解读考点精练系列答案