题目内容
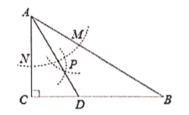
【题目】如图,抛物线y=﹣x2+2mx+m+2的图象与x轴交于A(﹣1,0),B两点,在x轴上方且平行于x轴的直线EF与抛物线交于E,F两点,E在F的左侧,过E,F分别作x轴的垂线,垂足是M,N.
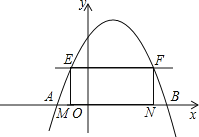
(1)求m的值及抛物线的顶点坐标;
(2)设BN=t,矩形EMNF的周长为C,求C与t的函数表达式;
(3)当矩形EMNF的周长为10时,将△ENM沿EN翻折,点M落在坐标平面内的点记为M',试判断点M'是否在抛物线上?并说明理由.
【答案】(1)y=﹣(x﹣1)2+4,顶点坐标为(1,4);(2)C=﹣2t2+4t+8;(3)点M'不在抛物线上.
【解析】
(1)因为抛物线上的点的坐标符合解析式,将A的坐标代入解析式即可求得m的值,进而求出解析式,即可求得顶点坐标;
(2)求出A、B两点坐标,可表示出MN的长,求出F点纵坐标,可知NF的长,利用矩形面积公式即可求出C与t的函数表达式;
(3)根据翻折变换的性质(翻折前后图形全等),结合勾股定理,求出M’点坐标,代入二次函数解析式验证.
(1)由于抛物线过点A(﹣1,0),
于是将A代入y=﹣x2+2mx+m+2
得﹣1﹣2m+m+2=0,
解得m=1,
函数解析式为y=﹣x2+2x+3,
解析式可化为y=﹣(x﹣1)2+4,顶点坐标为(1,4).
(2)因为函数解析式为y=﹣x2+2x+3,
所以当y=0时可得﹣x2+2x+3=0,解得x1=﹣1,x2=3,
则AB=3﹣(﹣1)=4.
又因为BN=t,M、N关于对称轴对称,
所以AM=t.于是MN=4﹣2t,
N点横坐标为3﹣t,代入抛物线得:yF=﹣t2+4t.
于是C=2(4﹣2t)﹣2(t﹣2)2+8,
整理得C=﹣2t2+4t+8;
(3)当﹣2t2+4t+8=10时,解得t=1,MN=4﹣2t=4﹣2=2;
FN=﹣12+4=3,
因为t=1,所以M与O点重合,
连接MM'、EN,且MM'和EN相交于K,根据翻折变换的性质,MK=M'K.
根据同一个三角形面积相等,2×3=![]() MK
MK
于是MK=![]() ,MM'=
,MM'=![]()
作M'H⊥MN的延长线于H.
设NH=a,HM′=b,
于是在Rt△NHM'和RT△MHM'中,
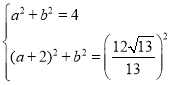 ,
,
解得a=![]() ,b=
,b=![]() .
.
于是MH=2+![]() =
=![]() .
.
M'点坐标为(![]() ,
,![]() ),
),
代入函数解析式y=﹣x2+2x+3,y=﹣x2+2x+3=﹣(![]() )2+2×
)2+2×![]() +3=
+3=![]() ≠
≠![]() ,
,
∴点M'不在抛物线上.

【题目】小涛根据学习函数的经验,对函数![]() 的图像与性质进行了探究,下面是小涛的探究过程,请补充完整:
的图像与性质进行了探究,下面是小涛的探究过程,请补充完整:
(1)下表是![]() 与
与![]() 的几组对应值
的几组对应值
| ... | -2 | -1 | 0 | 1 | 2 |
| 3 | ... |
| ... | -8 | -3 | 0 | m | n | 1 | 3 | ... |
请直接写出:![]() =, m=, n=;
=, m=, n=;
(2)如图,小涛在平面直角坐标系中,描出了上表中已经给出的部分对应值为坐标的点,再描出剩下的点,并画出该函数的图象;
(3)请直接写出函数![]() 的图像性质:;(写出一条即可)
的图像性质:;(写出一条即可)
(4)请结合画出的函数图象,解决问题:若方程![]() 有三个不同的解,直接写出
有三个不同的解,直接写出![]() 的取值范围.
的取值范围.