题目内容
如图,△ABC中,E、F分别是AB、AC上的点.
①AD平分∠BAC,②DE⊥AB,DF⊥AC,③AD⊥EF.
以此三个中的两个为条件,另一个为结论,可构成三个命题,即:
①②?③,①③?②,②③?①.
(1)试判断上述三个命题是否正确(直接作答);
(2)请证明你认为正确的命题.
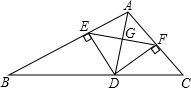
①AD平分∠BAC,②DE⊥AB,DF⊥AC,③AD⊥EF.
以此三个中的两个为条件,另一个为结论,可构成三个命题,即:
①②?③,①③?②,②③?①.
(1)试判断上述三个命题是否正确(直接作答);
(2)请证明你认为正确的命题.

(1)①②?③,正确;①③?②,错误,不符合三角形的判定;②③?①,正确.
(2)先证①②?③.如图.
∵AD平分∠BAC,DE⊥AB,DF⊥AC,AD=AD,
∴Rt△ADE≌Rt△ADF.
∴DE=DF,∠ADE=∠ADF.
设AD与EF交于G,则△DEG≌△DFG,
∴∠DGE=∠DGF.
∴∠DGE=∠DGF=90°.
∴AD⊥EF.
再证②③?①.如图2,

设AD的中点为O,连接OE,OF,
∵DE⊥AB,DF⊥AC,
∴OE,OF分别是Rt△ADE,Rt△ADF斜边上的中线.
∴OE=
AD,OF=
AD.
即点O到A、E、D、F的距离相等.
∴四点A、E、D、F在以O为圆心,
AD为半径的圆上,AD是直径.
∴EF是⊙O的弦.
∵EF⊥AD,
∴∠DAE=∠DAF.
即AD平分∠BAC.
(2)先证①②?③.如图.
∵AD平分∠BAC,DE⊥AB,DF⊥AC,AD=AD,
∴Rt△ADE≌Rt△ADF.
∴DE=DF,∠ADE=∠ADF.
设AD与EF交于G,则△DEG≌△DFG,
∴∠DGE=∠DGF.
∴∠DGE=∠DGF=90°.
∴AD⊥EF.
再证②③?①.如图2,

设AD的中点为O,连接OE,OF,
∵DE⊥AB,DF⊥AC,
∴OE,OF分别是Rt△ADE,Rt△ADF斜边上的中线.
∴OE=
| 1 |
| 2 |
| 1 |
| 2 |
即点O到A、E、D、F的距离相等.
∴四点A、E、D、F在以O为圆心,
| 1 |
| 2 |
∴EF是⊙O的弦.
∵EF⊥AD,
∴∠DAE=∠DAF.
即AD平分∠BAC.

练习册系列答案
 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案
相关题目



 底座的塑像,并且留出最窄处为1.6m的观光通道,问塑像底座的半径最大是多少?
底座的塑像,并且留出最窄处为1.6m的观光通道,问塑像底座的半径最大是多少?