��Ŀ����
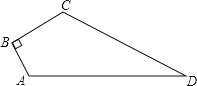
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У���A��B������ֱ�ΪA��a��0����B��n��0����a��n����|a+2|+![]() =0����ͬʱ����A��B�ֱ�����ƽ��4����λ��������ƽ��3����λ���ֱ�õ���A��B�Ķ�Ӧ��C��D������AC��BD��CD��
=0����ͬʱ����A��B�ֱ�����ƽ��4����λ��������ƽ��3����λ���ֱ�õ���A��B�Ķ�Ӧ��C��D������AC��BD��CD��
��1�����C��D�����꼰�ı���OBDC�������
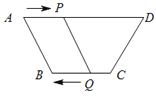
��2����ͼ2���� ��P���߶�BD�ϵ�һ�����㣬����PC��PO������P��BD���ƶ�ʱ������B��D�غϣ�![]() ��ֵ�Ƿ����仯����˵�����ɣ�
��ֵ�Ƿ����仯����˵�����ɣ�
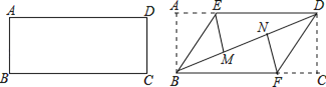
��3�����ı���OBDC���Ƿ����һ��P������PO��PB��PC��PD��ʹS��PCD=S��PBD�� S��POB��S��POC=1������������һ�㣬�����P�����꣬�������ڣ���˵�����ɣ�

���𰸡���1��24��2����ֵ���䣬1��3�����ڣ�P��3��2��
��������
��1�����ݱ��������;���ֵ���ڵ���0��ʽ���b��n���Ӷ��õ�A��B�����꣬�ٸ�������ƽ��4����λ�����������4������ƽ��3����λ����������3�������C��D�����꼴�ɣ�Ȼ������ƽ���ı��ε������ʽ����ʽ���㣻
��2������ƽ�Ƶ����ʿɵ�AB��CD���ٹ���P��PE��AB������ƽ�й����ɵ�PE��CD��Ȼ�������ֱ��ƽ�У��ڴ�����ȿɵá�DCP=��CPE����BOP=��OPE��Ȼ�������CPO=��DCP+��BOP���Ӷ��жϳ���ֵ���䣻
��3�����������ȵ������Կ�֪����PΪƽ���ı���ABCD�Խ��ߵĽ��㣬��PB=PC����˸����е�������P�����꣮
��1����ͼ1��
������ã�a+2=0��a=��2����A����2��0����
5��n=0��n=5����B��5��0����
�ߵ�A��B�ֱ�����ƽ��4����λ��������ƽ��3����λ��
���C��1��4����D��8��4����
��OB=5��CD=8��1=7��
��S�ı���OBDC=![]() ��CD+OB����h=
��CD+OB����h=![]() ��4����5+7��=24��
��4����5+7��=24��
��2��![]() ��ֵ�������仯����ֵΪ1�������ǣ�
��ֵ�������仯����ֵΪ1�������ǣ�
��ƽ�Ƶ����ʿɵ�AB��CD��
��ͼ2������P��PE��AB����AC��E����PE��CD��
���DCP=��CPE����BOP=��OPE��
���CPO=��CPE+��OPE=��DCP+��BOP��
��![]() =1����ֵ������
=1����ֵ������
��3�����ڣ���ͼ3������AD��BC���ڵ�P��
��AB=CD��AB��CD��
���ı���ABCD��ƽ���ı��Σ�
��BP=CP��
��S��PCD=S��PBD�� S��POB��S��POC=1��
��C��1��4����B��5��0��
��P��3��2����

 ��У����ϵ�д�
��У����ϵ�д�