题目内容
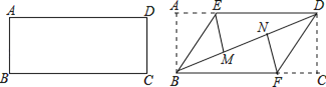
【题目】准备一张矩形纸片，按如图操作：将△ABE沿BE翻折，使点A落在对角线BD上的M点，将△CDF沿DF翻折，使点C落在对角线BD上的N点．
（1）求证：四边形BFDE是平行四边形.
（2）若四边形BFDE是菱形，BE =2，求菱形BFDE的面积．
【答案】（1）见解析；（2）2
【解析】分析：（1）根据矩形的性质和翻折变换的性质得到∠EBD=∠FDB，证明EB∥DF，根据平行四边形的判定定理证明结论；
（2）根据菱形的性质和翻折变换的性质求出∠ABE=30°，根据直角三角形的性质求出AB=
，根据菱形的面积公式计算即可．
详解：（1）∵四边形ABCD是矩形，∴∠A=∠C=90°，AB=CD，AB∥CD，∴∠ABD=∠CDB，由翻折变换的性质可知，∠ABE=∠EBD，∠CDF=∠FDB，∴∠EBD=∠FDB，∴EB∥DF．
∵ED∥BF，∴四边形BFDE为平行四边形；
（2）∵四边形BFDE为菱形，∴∠EBD=∠FBD．
∵∠EBD=∠ABE，∴∠EBD=∠FBD=∠ABE．
∵四边形ABCD是矩形，∠ABC=90°，∴∠EBD=∠FBD=∠ABE=30°，∴AB=
，∴菱形BFDE的面积S=DE×AB=2
．
练习册系列答案
相关题目
