题目内容
【题目】已知等边△ABC的边长为2,点D在射线CB上,点E在射线AC上,且AD=AE,∠EDC=15°,则线段CD=_______.
【答案】1或4
【解析】
如图1和图2,分点D、点E分别在线段CB和AC上和点D、点E分别在CB的延长线和AC的延长线上两种情形画出符合题意的图形,再结合已知条件分别进行分析解答即可.
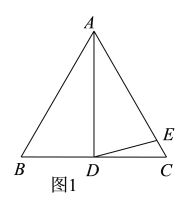
(1)如图1,当点D、点E分别在线段CB和AC上时,
∵△ABC是等边三角形,
∴∠C=∠BAC=60°,
∵∠CDE=15°,
∴∠AED=∠CDE+∠C=15°+60°=75°,
∵AD=AE,
∴∠AED=∠AED=75°,
∴∠DAE=180°-75°-75°=30°,
∴∠BAD=60°-30°=30°=∠CAD,
∴AD是等边三角形BC边上的中线,
∴CD=![]() BC=1;
BC=1;
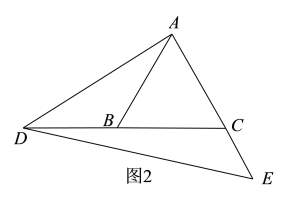
(2)如图2,当点D、点E分别在CB的延长线和AC的延长线上时,
∵△ABC是等边三角形,
∴∠ACB =60°,
∵∠CDE=15°,
∴∠E=∠ACB-∠CDE=60°-15°=45°,
∵AD=AE,
∴∠ADE=∠E=45°,
∴∠DAE=180°-45°-45°=90°,
∴∠ADC=180°-∠DAE-∠ACB=30°,
∴CD=2AC=4.
综合(1)(2)可得:CD=1或4.
故答案为:1或4.

【题目】列方程解应用题:五莲县新玛特购物中心第一次用5000元购进甲、乙两种商品,其中乙商品的件数比甲商品件数的![]() 倍多15件,甲、乙两种商品的进价和售价如下表(注:获利=售价﹣进价)
倍多15件,甲、乙两种商品的进价和售价如下表(注:获利=售价﹣进价)
甲 | 乙 | |
进价(元/件) | 20 | 30 |
售价(元/件) | 29 | 40 |
(1)新玛特购物中心将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润?
(2)该购物中心第二次以第一次的进价又购进甲、乙两种商品,其中甲种商品的件数不变,乙种商品的件数是第一次的3倍;甲商品按原价销售,乙商品打折销售,第二次两种商品都销售完以后获得总利润比第一次获得的总利润多160元,求第二次乙种商品是按原价打几折销售?