题目内容
【题目】如图,在△ABC中,AB=BC,BD平分∠ABC.过点D作AB的平行线,过点B作AC的平行线,两平行线相交于点E, BC交DE于点F,连接CE.求证:四边形BECD是矩形.
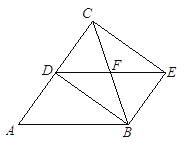
【答案】证明见解析.
【解析】根据已知条件易推知四边形BECD是平行四边形. 结合等腰△ABC“三线合一”的性质证得BD⊥AC,即∠BDC=90°,所以由“有一内角为直角的平行四边形是菱形”得到◇BECD是矩形.
解:∵AB=BC,BD平分∠ABC
∴AD=DC,BD⊥CA
∵AB∥DE, AD∥BE
∴四边形ABED是平行四边形
∴AD=BE,AD∥BE, AB=DE
∴DC=BE,DC∥BE
∴四边形BECD是平行四边形
∵BD⊥CA
∴∠BDC=90°![]()
∴四边形BECD是矩形

练习册系列答案
相关题目