Question

【题目】如图1，抛物线与x轴交于A、B两点（A在B的左侧），与y轴正半轴交于点C，抛物线的顶点为P，对称轴为直线，且OC＝3OA．

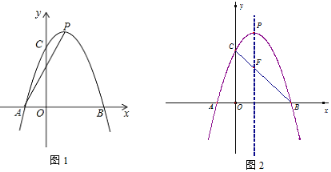
（1）求抛物线的解析式；

（2）点D（2，m）在抛物线上，点E在直线AP上，使DE⊥OE，求点E的横坐标；

（3）如图2，连接BC与抛物线的对称轴交于点F，在抛物线上是否存在点G，使△GPF与△GBF的面积相等，若存在，求出点G坐标；若不存在，请说明理由．

Answer 1

【答案】（1）抛物线的解析式为：.

（2）E点的横坐标为

（3）理由见详解.

【解析】

（1）利用抛物线的对称轴方程求出b，利用OC＝3OA确定c的值，从而得到抛物线解析式.

（2）先求出D点坐标为（2，3），则AP上一点E，作EM⊥OB，DN⊥EM，则△EMO∽△DNE，得，设E（x，y），列出方程即可解决问题．
（3）设G（m，-m2+2m+3），根据，列出方程即可解决问题，当G′在x轴下方时，方法类似．

解（1）∵抛物线的对称轴为直线x=1，
∴ ，解得b=2

∴抛物线的解析式为：

设A点坐标为：（a，0），（a<0），C点坐标为：（0，c）, （c>0）则有：

解之得：（取负数）

又∵OC＝3OA

∴

∴

解之得：

∴抛物线的解析式为：

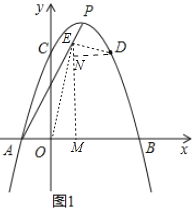
（2）

将D（2，m）代入抛物线的解析式为：得：

∴D点坐标为（2，3）

如图1，点E在直线AP上，DE⊥OE，作EM⊥OB，DN⊥EM，
则△EMO∽△DNE，
∴ ，
设E（x，y），
则 ，
∴
又∵，
解得：，

∴E点的横坐标为

；
（3）

由得F(1,2),B(3,0),P(1,4)

存在点G，使△GPF与△GBF的面积相等.

如图2所示，设G（m，-m2+2m+3），
∵，
∴ ，
解得或，

当时，

∴

当时，

∴点G坐标（，2），或（，2）
当G′在x轴下方时，且在对称轴的右侧时，有

，
解得或（舍弃），

∴
∴点G坐标（，），

当G′在x轴下方时，且在对称轴的左侧时，有

解得： ,则，不符合题意舍去.
∴使△GPF与△GBF的面积相等点G的坐标为，（，2），（，2）（，）．