题目内容
已知:如图, 中,
中, ,以
,以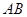 为直径的⊙O交
为直径的⊙O交 于点
于点 ,
, 于点
于点 .
.

(1)求证:PD是⊙O的切线;
(2)若AB="2" ,∠CAB=120°,求 BC的值.
 中,
中, ,以
,以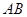 为直径的⊙O交
为直径的⊙O交 于点
于点 ,
, 于点
于点 .
.
(1)求证:PD是⊙O的切线;
(2)若AB="2" ,∠CAB=120°,求 BC的值.
(1)连接OP,要证明PD是⊙O的切线只要证明∠DPO=90°即可;(2)2

试题分析:(1)连接OP,要证明PD是⊙O的切线只要证明∠DPO=90°即可;
(2)连接AP,根据已知可求得BP的长,从而可求得BC的长.
(1)连接OP
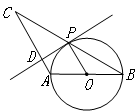
∵AB是直径
∴∠APB=90°
∵AB=AC
∴BP=CP
∵BO=OA
∴PO∥AC
∵PD⊥AC
∴PD⊥PO
∴PD为切线;
(2)连接AP

∵AB=2
∴AC=2
OA=OB=OP=1
∵∠CAB=120°
又AP⊥BC,AB=AC
∴∠PAB=60°
∴AP=OA=OP=1,
∴BP=

∴BC=2

点评:要证某线是圆的切线,已知此线过圆上某点,连接圆心和这点(即为半径),再证垂直即可.

练习册系列答案
 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案
相关题目
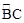 的长为 cm.
的长为 cm.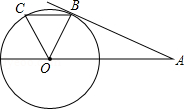
 =
= ,点E为OD上任意一点(不与O、D重合).求证:AE=BE.
,点E为OD上任意一点(不与O、D重合).求证:AE=BE.
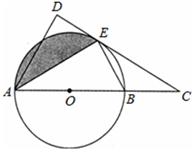
 中,AB=10,AC=8,BC=6,经过点C且与边AB相切的动圆与CA,CB分别相交于点P,Q,则线段PQ长度的最小值是
中,AB=10,AC=8,BC=6,经过点C且与边AB相切的动圆与CA,CB分别相交于点P,Q,则线段PQ长度的最小值是 

 ),若⊙P与⊙Q的半径分别是3和2,则⊙P与⊙Q的位置关系是( )
),若⊙P与⊙Q的半径分别是3和2,则⊙P与⊙Q的位置关系是( ) 和3
和3