题目内容
若一个矩形的一边是另一边的两倍,则称这个矩形为方形,如图1,矩形ABCD中,BC=2AB,则称ABCD为方形.
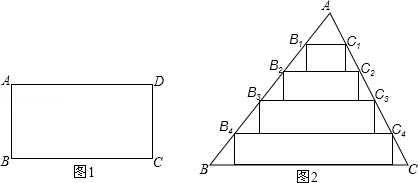
(1)设a,b是方形的一组邻边长,写出a,b的值(一组即可).
(2)在△ABC中,将AB,AC分别五等分,连结两边对应的等分点,以这些连结为一边作矩形,使这些矩形的边B1C1,B2C2,B3C3,B4C4的对边分别在B2C2,B3C3,B4C4,BC上,如图2所示.
①若BC=25,BC边上的高为20,判断以B1C1为一边的矩形是不是方形?为什么?
②若以B3C3为一边的矩形为方形,求BC与BC边上的高之比.

(1)设a,b是方形的一组邻边长,写出a,b的值(一组即可).
(2)在△ABC中,将AB,AC分别五等分,连结两边对应的等分点,以这些连结为一边作矩形,使这些矩形的边B1C1,B2C2,B3C3,B4C4的对边分别在B2C2,B3C3,B4C4,BC上,如图2所示.
①若BC=25,BC边上的高为20,判断以B1C1为一边的矩形是不是方形?为什么?
②若以B3C3为一边的矩形为方形,求BC与BC边上的高之比.
(1)答案不唯一,a=2,b=4(2)①以B1C1为一边的矩形不是方形② 或
或
 或
或
解:(1)答案不唯一,如a=2,b=4。
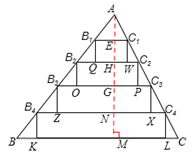
(2)①以B1C1为一边的矩形不是方形。理由如下:
过A作AM⊥BC于M,交B1C1于E,交B2C2于H,交B3C3于G,交B4C4于N,则AM⊥B4C4,AM⊥B3C3,AM⊥B2C2,AM⊥B1C1,
∵由矩形的性质得:BC∥B1C1∥B2C2∥B3C3∥B4C4,
∴△ABC∽△AB1C1∽△AB2C2∽△AB3C3∽△AB4C4,
∴ 。
。
∵AM=20,BC=25,
∴B1C1=5,B2C2=10,B3C3=15,B4C4=20,AE=4,AH=8,AG=12,AN=16。
∴MN=GN=GH=HE=4。∴BQ=B2O=B3Z=B4K=4,即B1C1≠2B1Q,B1Q≠2B1C1。
∴以B1C1为一边的矩形不是方形。
②设AM=h,
∵以B3C3为一边的矩形为方形,∴△ABC∽△AB3C3。,∴ 。
。
∴AG= h。∴MN=GN=GH=HE=
h。∴MN=GN=GH=HE=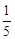 h。
h。
当B3C3=2×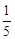 h,时,
h,时,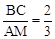 ;
;
当B3C3=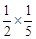 h时,
h时,
综合上述:BC与BC边上的高之比是 或
或 。
。
(1)答案不唯一,根据已知举出即可。
(2)①求出△ABC∽△AB1C1∽△AB2C2∽△AB3C3∽△AB4C4,推出 ,
, ,求出B1C1=5,B2C2=10,B3C3=15,B4C4=20,AE=4,AH=8,AG=12,AN=16,MN=GN=GH=HE=4,BQ=B2O=B3Z=B4K=4,根据定义判断即可。
,求出B1C1=5,B2C2=10,B3C3=15,B4C4=20,AE=4,AH=8,AG=12,AN=16,MN=GN=GH=HE=4,BQ=B2O=B3Z=B4K=4,根据定义判断即可。
②设AM=h,根据△ABC∽△AB3C3,得出 ,求出MN=GN=GH=HE=
,求出MN=GN=GH=HE=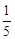 h,分为两种情况:当B3C3=2×
h,分为两种情况:当B3C3=2×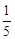 h,时,当B3C3=
h,时,当B3C3=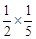 h时,代入求出即可。
h时,代入求出即可。

(2)①以B1C1为一边的矩形不是方形。理由如下:
过A作AM⊥BC于M,交B1C1于E,交B2C2于H,交B3C3于G,交B4C4于N,则AM⊥B4C4,AM⊥B3C3,AM⊥B2C2,AM⊥B1C1,
∵由矩形的性质得:BC∥B1C1∥B2C2∥B3C3∥B4C4,
∴△ABC∽△AB1C1∽△AB2C2∽△AB3C3∽△AB4C4,
∴
 。
。∵AM=20,BC=25,
∴B1C1=5,B2C2=10,B3C3=15,B4C4=20,AE=4,AH=8,AG=12,AN=16。
∴MN=GN=GH=HE=4。∴BQ=B2O=B3Z=B4K=4,即B1C1≠2B1Q,B1Q≠2B1C1。
∴以B1C1为一边的矩形不是方形。
②设AM=h,
∵以B3C3为一边的矩形为方形,∴△ABC∽△AB3C3。,∴
 。
。∴AG=
 h。∴MN=GN=GH=HE=
h。∴MN=GN=GH=HE=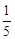 h。
h。当B3C3=2×
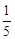 h,时,
h,时,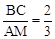 ;
;当B3C3=
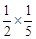 h时,
h时,
综合上述:BC与BC边上的高之比是
 或
或 。
。(1)答案不唯一,根据已知举出即可。
(2)①求出△ABC∽△AB1C1∽△AB2C2∽△AB3C3∽△AB4C4,推出
 ,
, ,求出B1C1=5,B2C2=10,B3C3=15,B4C4=20,AE=4,AH=8,AG=12,AN=16,MN=GN=GH=HE=4,BQ=B2O=B3Z=B4K=4,根据定义判断即可。
,求出B1C1=5,B2C2=10,B3C3=15,B4C4=20,AE=4,AH=8,AG=12,AN=16,MN=GN=GH=HE=4,BQ=B2O=B3Z=B4K=4,根据定义判断即可。②设AM=h,根据△ABC∽△AB3C3,得出
 ,求出MN=GN=GH=HE=
,求出MN=GN=GH=HE=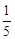 h,分为两种情况:当B3C3=2×
h,分为两种情况:当B3C3=2×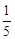 h,时,当B3C3=
h,时,当B3C3=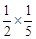 h时,代入求出即可。
h时,代入求出即可。 
练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目

 ,BC=3,△DEF是边长为a(a为小于3的常数)的等边三角形,将△DEF沿AC方向平移,使点D在线段AC上,DE∥AB,设△DEF与△ABC重叠部分的周长为T。
,BC=3,△DEF是边长为a(a为小于3的常数)的等边三角形,将△DEF沿AC方向平移,使点D在线段AC上,DE∥AB,设△DEF与△ABC重叠部分的周长为T。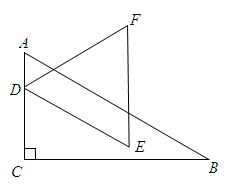
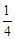 ,当a=2时,求T的值;
,当a=2时,求T的值;



 的根,则判别式△=b2-4ac和完全平方式M=
的根,则判别式△=b2-4ac和完全平方式M= 的关系是( )
的关系是( )