��Ŀ����
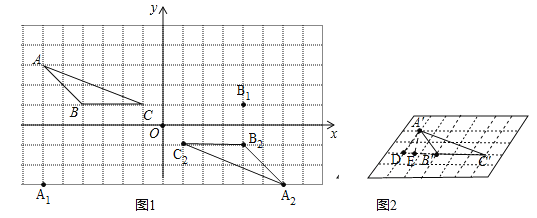
����Ŀ����ƽ��ֱ������ϵ�У�A��B��C����������ֱ�ΪA����6��3����B����4��1����C����1��1����
��1����ͼ1��˳������AB��BC��CA������ABC��
����A����x��ĶԳƵ�A1�������� ����B����y��ĶԳƵ�B1�������� ��
��������ABC����ԭ��ԳƵ���A2B2C2��
��tan��A2C2B2= ��
��2�������ı��εIJ��ȶ��ԣ����ڶ���������С��������ɵ����仯Ϊ��ͼ2��ʾ����С������ɵ�����ÿ��С���εı߳���Ϊ1����λ���ȣ��ҽ�С�ڽ�Ϊ60����ԭ���ĸ��A��B��C�ֱ��Ӧ�������еĸ��A����B����C����˳������A��B����B��C����C��A��������A��B��C������tan��A��C��B��= ��

���𰸡���1���٣���6����3������4��1�����ڴ𰸼���������![]() ����2��
����2��![]() ��
��
�������������������1����ֱ�ӵõ��ԳƵ�����꼴�ɣ�
����ͼ��
���������еĶ��壺���ڶԱ߱��ڱߣ���tan��A2B2C2=![]() ��
��
��2��������A'E������ֱ�������Σ����ù��ɶ�����A'E��EC'�ij����ɵý��ۣ�
����������⣺��1������A����x��ĶԳƵ�A1�������ǣ���6����3������B����y��ĶԳƵ�B1�������ǣ�4��1����
�ʴ�Ϊ������6����3������4��1����
����ͼ1��ʾ��
��tan��A2B2C2=![]() ���ʴ�Ϊ��
���ʴ�Ϊ�� ![]() ��
��
��2����ͼ2����A'��A'E��B��C����E���ӳ�C��B����D��ʹDC'=5������A'D��Rt��A��ED�У��ߡ�A��DE=60����A'D=2����DE=1��A'E=![]() ����EC'=5��1=4��Rt��A��EC���У�tan��A'C'B'=
����EC'=5��1=4��Rt��A��EC����tan��A'C'B'=![]() =
=![]() ���ʴ�Ϊ��
���ʴ�Ϊ�� ![]() ��
��

 �������¿��ÿ�ʱ��ҵϵ�д�
�������¿��ÿ�ʱ��ҵϵ�д� Ӣ�żƻ�ͬ����ʱ��Чѵ��ϵ�д�
Ӣ�żƻ�ͬ����ʱ��Чѵ��ϵ�д�