题目内容
【题目】已知关于x、y的方程组 
的解满足x＞0，y＞0，求实数a的取值范围．
【答案】解：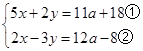 
， ①×3得，15x+6y=33a+54③，
②×2得，4x﹣6y=24a﹣16④，
③+④得，19x=57a+38，
解得x=3a+2，
把x=3a+2代入①得，5（3a+2）+2y=11a+18，
解得y=﹣2a+4，
所以，方程组的解是 
，
∵x＞0，y＞0，
∴ 
，
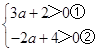由①得，a＞﹣ 
，
由②得，a＜2，
所以，a的取值范围是﹣ ＜a＜2．
【解析】先利用加减消元法求出x、y，然后列出不等式组，再求出两个不等式的解集，然后求公共部分即可．
【考点精析】解答此题的关键在于理解解二元一次方程组的相关知识，掌握二元一次方程组：①代入消元法；②加减消元法，以及对一元一次不等式组的解法的理解，了解解法：①分别求出这个不等式组中各个不等式的解集；②利用数轴表示出各个不等式的解集；③找出公共部分；④用不等式表示出这个不等式组的解集．如果这些不等式的解集的没有公共部分，则这个不等式组无解 ( 此时也称这个不等式组的解集为空集 )．
【题目】某饮料厂生产一种饮料，经测算，用1吨水生产的饮料所获利润y（元）是1吨水的价格x（元）的一次函数．
（1）根据下表提供的数据，求y与x的函数关系式；当水价为每吨10元时，1吨水生产出的饮料所获的利润是多少？
1吨水价格x（元） | 4 | 6 |
用1吨水生产的饮料所获利润y（元） | 200 | 198 |
（2）为节约用水，这个市规定：该厂日用水量不超过20吨时，水价为每吨4元；日用水量超过20吨时，超过部分按每吨40元收费．已知该厂日用水量不少于20吨，设该厂日用水量为t吨，当日所获利润为W元，求W与t的函数关系式；该厂加强管理，积极节水，使日用水量不超过25吨，但仍不少于20吨，求该厂的日利润的取值范围．
