题目内容
【题目】如图,AD是圆O的切线,切点为A,AB是圆O的弦。过点B作BC//AD,交圆O于点C,连接AC,过点C作CD//AB,交AD于点D。连接AO并延长交BC于点M,交过点C的直线于点P,且BCP=ACD。
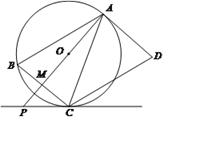
(1) 判断直线PC与圆O的位置关系,并说明理由:
(2) 若AB=9,BC=6,求PC的长。
【答案】(1)相切;证明见解析;(2)![]() .
.
【解析】试题分析:(1)通过分析,直线与圆O已经有一个公共点,连接半径0C,只要证明OC⊥PC即可;(2)根据AD是切线和AD∥BC证明AP⊥BC,利用垂径定理计算出CM=BM=3,在Rt△AMB中,利用勾股定义计算出AM的长,在Rt△OMC中,利用勾股定理建立方程计算出圆O的半径的长,最后证明△OMC~△OCP,利用相似三角形的对应边成比例计算出PC的长.
试题解析:(1) 直线PC与圆O相切.
连接CO并延长,交圆O于点N,连接BN.
∵AB//CD,
∴BAC=ACD.
∵BAC=BNC,
∴BNC=ACD.
∵BCP=ACD,
∴BNC=BCP.
∵CN是圆O的直径,
∴CBN=90°.
∴BNC+BCN=90°,
∴BCP+BCN=90°.
∴PCO=90°,即PC^OC.
又∵点C在圆O上,
∴直线PC与圆O相切.
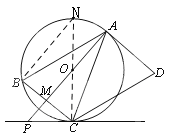
(2) ∵AD是圆O的切线,
∴AD^OA,即OAD=90°.
∵BC//AD,
∴OMC=180°-OAD=90°,即OM^BC.
∴MC=MB.
∴AB=AC.
在Rt△AMC中,AMC=90°,AC=AB=9,MC=![]() BC=3,
BC=3,
由勾股定理,得AM=![]() =
=![]() =6
=6![]() .
.
设圆O的半径为r.
在Rt△OMC中,OMC=90°,OM=AM-AO=6![]() -r,MC=3,OC=r,
-r,MC=3,OC=r,
由勾股定理,得OM 2+MC 2=OC 2,
∴(6![]() -r)2+32=r2.
-r)2+32=r2.
解得r=![]() .
.
在△OMC和△OCP中,
∵OMC=OCP,MOC=COP,
∴△OMC~△OCP.
∴![]() =
=![]() ,即
,即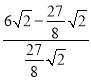 =
=![]() .
.
∴PC=![]() .
.

【题目】某市甲、乙两个汽车销售公司,去年一至十月份每月销售同种品牌汽车的情况如图所示: 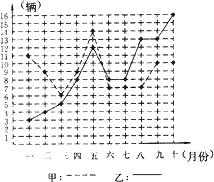
(1)请你根据上图填写下表:
销售公司 | 平均数 | 方差 | 中位数 | 众数 |
甲 | 5.2 | 9 | ||
乙 | 9 | 17.0 | 8 |
(2)请你从以下两个不同的方面对甲、乙两个汽车销售公司去年一至十月份的销售情况进行分析: ①从平均数和方差结合看;
②从折线图上甲、乙两个汽车销售公司销售数量的趋势看(分析哪个汽车销售公司较有潜力).