题目内容
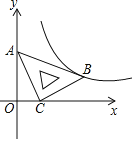
【题目】如图,一次函数y=ax+b的图像与正比例函数y=kx的图像交于点M,
(1)求正比例函数和一次函数的解析式;
(2)根据图像写出使正比例函数的值大于一次函数的值的x的取值范围;
(3)求ΔMOP的面积。
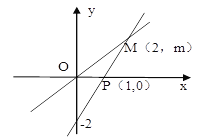
【答案】(1)一次函数表达式为: y=2x-2;正比例函数为 y=x;(2)x<2;(3)1.
【解析】∵y=ax+b经过(1,0)和(0,-2)
∴![]() …………………………………………………1分
…………………………………………………1分
解得:k=2 b=-2…………………………………………..2分
一次函数表达式为: y=2x-2…………………………………3分
∵点M在该一次函数上,∴m=2 x 2-2=2
M点坐标为(2,2)……………………………………………4分
又∵M在函数 y=kx上,∴ k=m/2=2/2=1
∴正比例函数为 y=x…………………………………………..5分
(2)由图像可知,当x=2时,一次函数与正比例函数相交;x<2时,正比例函数图像在一次函数上方,故:
x<2时,x>2x-2………………………………………………….7分
(3)作MN垂直X轴,易知MN=2
∴故SΔMOP=1/2 x 1 x 2=1

 阅读快车系列答案
阅读快车系列答案【题目】某中学八年级组织了一次“汉字听写比赛”,每班选25名同学参加比赛,成绩分为A,B,C,D四个等级,其中A等级得分为100分,B等级得分为85分,C等级得分为75分,D等级得分为60分,语文教研组将八年级一班和二班的成绩整理并绘制成如下的统计图,请根损换供的信息解答下列问题.
(1)把一班比赛成统计图补充完整;

(2)填表:
平均数(分) | 中位数(分) | 众数(分) | |
一班 | a | b | 85 |
二班 | 84 | 75 | c |
表格中:a=______,b=______,c=_______.
(3)请从以下给出的两个方面对这次比赛成绩的结果进行分析:
①从平均数、众数方面来比较一班和二班的成绩;
②从B级以上(包括B级)的人数方面来比较-班和二班的成绩.