题目内容
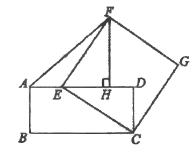
【题目】如图,在矩形ABCD中,AD=4,点E在边AD上,连接CE,以CE为边向右上方作正方形CEFG,作FH⊥AD,垂足为H,连接AF.
(1)求证:FH=ED;
(2)当AE为何值时,△AEF的面积最大?
【答案】(1)见解析;(2)AE=2.
【解析】
(1)根据正方形的性质,可得EF=CE,再根据∠CEF=∠90°,进而可得∠FEH=∠DCE,结合已知条件∠FHE=∠D=90°,利用“AAS”即可证明△FEH≌△ECD,由全等三角形的性质可得FH=ED;
(2)设AE=a,用含a的函数表示△AEF的面积,再利用函数的最值求面积最大值即可.
(1)证明:
∵四边形CEFG是正方形,
∴CE=EF,
∵∠FEC=∠FEH+∠CED=90°,∠DCE+∠CED=90°,
∴∠FEH=∠DCE,
在△FEH和△ECD中
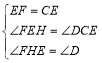 ,
,
∴△FEH≌△ECD,
∴FH=ED;
(2)设AE=a,则ED=FH=4a,
∴S![]() =
=![]() AEFH=
AEFH=![]() a(4a),
a(4a),
=![]() (a2)
(a2)![]() +2,
+2,
∴当AE=2时,△AEF的面积最大.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目