题目内容
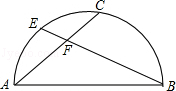
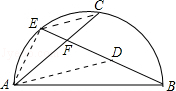
如图,AB是半圆的直径,点C是弧AB的中点,点E是弧AC的中点,连接EB,CA交于点F,则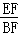 =( )
=( )
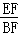 =( )
=( )
A. | B.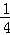 | C.1﹣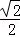 | D.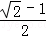 |
D
连接AE、CE,作AD∥CE,交BE于D.
∵点E是弧AC的中点
∴可设AE=CE=1,
根据平行线的性质得∠ADE=∠E=45°.
∴△ADE是等腰直角三角形,
则AD=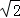 ,BD=AD=
,BD=AD=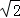 .
.
所以BE=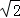 +1.
+1.
再根据两角对应相等得△AEF∽△BEA,
则EF=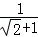 =
=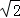 ﹣1,BF=2.
﹣1,BF=2.
所以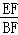 =
=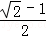 .
.
故选D.
∵点E是弧AC的中点
∴可设AE=CE=1,
根据平行线的性质得∠ADE=∠E=45°.
∴△ADE是等腰直角三角形,
则AD=
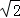 ,BD=AD=
,BD=AD=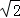 .
.所以BE=
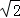 +1.
+1.再根据两角对应相等得△AEF∽△BEA,
则EF=
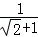 =
=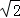 ﹣1,BF=2.
﹣1,BF=2.所以
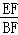 =
=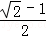 .
.故选D.


练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
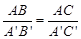 ,∠A=∠B'
,∠A=∠B'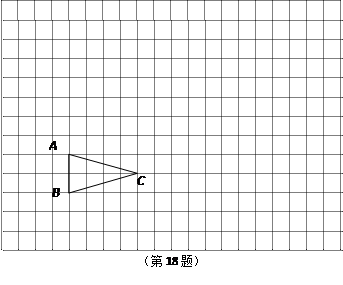
 相似(至少找出两个满足条件的点的坐标).
相似(至少找出两个满足条件的点的坐标).
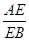 =
=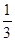 ,则
,则 的值为 【 】
的值为 【 】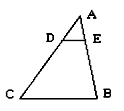
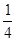 C、
C、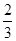 D、
D、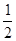
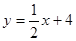 的图象与该二次函数的图象交于
的图象与该二次函数的图象交于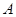 点(8,8),直线与
点(8,8),直线与 轴的交点为C,与y轴的交点为B.
轴的交点为C,与y轴的交点为B.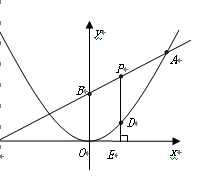
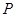 为线段
为线段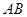 上的一个动点(点
上的一个动点(点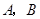 不重合),过
不重合),过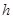 ,点
,点 相似?若存在,请求出
相似?若存在,请求出