题目内容
【题目】已知,菱形![]() 中,
中,![]() ,
,![]() 、
、![]() 分别是边
分别是边![]() 和
和![]() 上的点,且
上的点,且![]() .
.
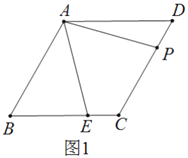
(1)求证:![]()
(2)如图2,![]() 在
在![]() 延长线上,且
延长线上,且![]() ,求证:
,求证:![]()
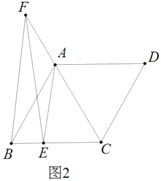
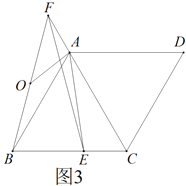
(3)如图3,在(2)的条件下,![]() ,
,![]() ,
,![]() 是
是![]() 的中点,求
的中点,求![]() 的长.
的长.
【答案】(1)证明见解析;(2)证明见解析;(3)7
【解析】
(1)连接AC,如图1,根据菱形的性质得AB=BC,而∠B=60°,则可判定△ABC为等边三角形,得到∠BAC=60°,AC=AB,易得∠ACF=60°,∠BAE=∠CAF,然后利用ASA可证明△AEB≌△AFC,即可解答;
(2)过点F作FH∥AB,交CB的延长线于点H,利用平行线的性质求得△FHC是等边三角形,得到CF=CH=FH,然后利用AAS定理求得△HBF≌△CEF,从而问题得解;
(3)过点B作BK∥FC,交HF于点K,根据两组对边分别平行求得四边形KBAF是平行四边形,从而求得![]() ,FK=16,过点A作AM⊥FH,然后利用含30°的直角三角形的性质求得MF=
,FK=16,过点A作AM⊥FH,然后利用含30°的直角三角形的性质求得MF=![]() ,
,![]() ,从而求得KM=13,然后利用勾股定理求解即可.
,从而求得KM=13,然后利用勾股定理求解即可.
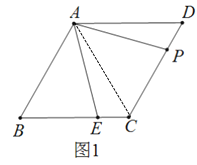
解:(1)连接AC,如图1,
∵四边形ABCD为菱形,
∴AB=BC,
∵∠B=60°,
∴△ABC为等边三角形,
∴∠BAC=60°,AC=AB,
∴∠BAE+∠EAC=60°,
∵AB∥CD,
∴∠BAC=∠ACP=60°,
∵∠EAP=60°,即∠EAC+∠CAP=60°,
∴∠BAE=∠CAP,
在△AEB和△APC中,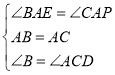 ,
,
∴△AEB≌△APC,
∴BE=CF
∴![]() ;
;
(2)过点F作FH∥AB,交CB的延长线于点H
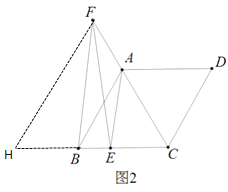
∵FH∥AB
∴∠H=∠CGH=60°
∴△FHC是等边三角形
∴CF=CH=FH
又∵△ABC是等边三角形
∴CA=CB
∴AF=BH
又∵FB=FE
∴∠FEB=∠FEB,即∠FBH=∠FEC
在△HBF和△CEF中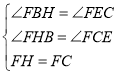
∴△HBF≌△CEF
∴BH=EC
∴AF=EC
(3)过点B作BK∥FC,交HF于点K,
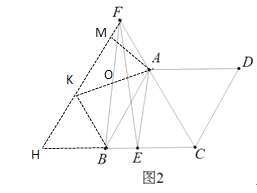
∵BK∥FC,FH∥AB
∴四边形KBAF是平行四边形
∴KB=AF=EC=6,![]()
∴FK=AB=BC=BE+EC=BE+AF=16
过点A作AM⊥FH
由(2)可知,∠CFH=60°
∴在Rt△AMF中,∠MAF=30°
∴MF=![]() ,
,![]()
∴KM=16-3=13
在Rt△AKM中,![]()
∴AO=7.

 出彩同步大试卷系列答案
出彩同步大试卷系列答案