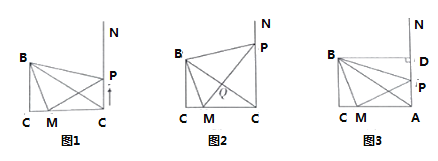
题目内容
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 在
在![]() 上,且
上,且![]() ,过点
,过点![]() 作射线
作射线![]() (AN与BC在AC同侧),若动点
(AN与BC在AC同侧),若动点![]() 从点
从点![]() 出发,沿射线
出发,沿射线![]() 匀速运动,运动速度为
匀速运动,运动速度为![]() /
/![]() ,设点
,设点![]() 运动时间为
运动时间为![]() 秒.
秒.
(1)经过_______秒时,![]() 是等腰直角三角形?
是等腰直角三角形?
(2)当![]() 于点
于点![]() 时,求此时
时,求此时![]() 的值;
的值;
(3)过点![]() 作
作![]() 于点
于点![]() ,已知
,已知![]() ,请问是否存在点
,请问是否存在点![]() ,使
,使![]() 是以
是以![]() 为腰的等腰三角形?对存在的情况,请求出t的值,对不存在的情况,请说明理由.
为腰的等腰三角形?对存在的情况,请求出t的值,对不存在的情况,请说明理由.
【答案】(1)6;(2)8;(3)2
【解析】
(1)得出两腰AM=AP时,即可得出答案;
(2)根据垂直的定义和同角的余角相等得到∠CBA=∠AMP,证明△ACB≌△PAM,得出比例式,代入求出AP,即可得出答案;
(3)由勾股定理求出BM的值,可知BD>BM,则不存在点P使![]() 的等腰三角形,又由AM<BM,则存在点P使
的等腰三角形,又由AM<BM,则存在点P使![]() 的等腰三角形,可证△MCB≌△PAM得PA的长,即可求出t的值.
的等腰三角形,可证△MCB≌△PAM得PA的长,即可求出t的值.
解:(1)∵∠PAM=90°,当![]() 是等腰直角三角形时,
是等腰直角三角形时,
则有PA=AM=6cm,
∴t=6÷1=6(s)
故答案为:6;
(2)∵![]() ,
,![]()
∴∠AQM=90°,∠PAM=90°,
∴∠AMP+∠BAC=90°,
又∵∠C=90°,
∴∠CBA+∠BAC=90°,
∴∠AMP=∠CBA,
在△ACB和△PAM中,
 ,
,
∴△ACB≌△PAM(ASA),
∴PA=AC,
∵![]() ,
,
∴![]() ,
,
∴t=8÷1=8(s),此时![]() 的值为8;
的值为8;
(3)∵![]() ,
,![]() ,
,![]() ,
, ![]() ,
,
∴![]() ,
,
由勾股定理得:![]() ,
,
∵![]() ,
,![]() ,
,
∴BD>BM,则不存在点P使![]() 的等腰三角形,
的等腰三角形,
又∵AM<BM,则存在点P使![]() 的等腰三角形,
的等腰三角形,
在Rt△MCB和Rt△PAM中,
![]() ,
,
∴△MCB≌△PAM(HL),
∴PA=CM=2cm,
∴t=2÷1=2(s),此时![]() 的值为2.
的值为2.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目