Question

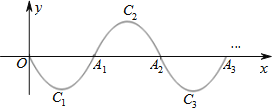
【题目】如图，一段抛物线：y＝x(x﹣2)(0≤x≤2)，记为C1，它与x轴交于点O，A1；将C1绕点A1旋转180°得C2，交x轴于点A2；将C2绕点A2旋转180°得C3，交x轴于点A3；…，如此进行下去，得到图形．

(1)请写出抛物线C2的解析式：_____．

(2)若点P(4037.5，a)在图形G上，则a＝_____．

Answer 1

【答案】 0.75

【解析】

（1）利用交点式得到A1（2，0），利用旋转的性质得A2（4，0），然后利用交点式写出抛物线C2的解析式；

（2）利用4037.5＝2018×2+1.5可判断点P在抛物线C2019上，而它的解析式为y＝（x﹣4036）（x﹣4038），然后计算把x＝4037.5对应的函数值即可．

（1）抛物线C1的解析式为y＝x（x﹣2），则A1（2，0），

根据旋转的性质得A1A2＝OA1＝2，则A2（4，0），

抛物线C2的解析式为y＝﹣（x﹣2）（x﹣4）；

（2）∵4037.5＝2018×2+1.5，

∴点P（4037.5，a）在抛物线C2019上，而抛物线C2019的解析式为y＝（x﹣4036）（x﹣4038）

把x＝4037.5代入得a＝（4037.5﹣4036）（4037.5﹣4038）＝0.75．

故答案为；0.75．