题目内容
【题目】综合与实践
![]() 纸是我们学习工作最常用的纸张之一, 其长宽之比是
纸是我们学习工作最常用的纸张之一, 其长宽之比是![]() ,我们定义:长宽之比是
,我们定义:长宽之比是![]() 的矩形纸片称为“标准纸”.
的矩形纸片称为“标准纸”.
操作判断:
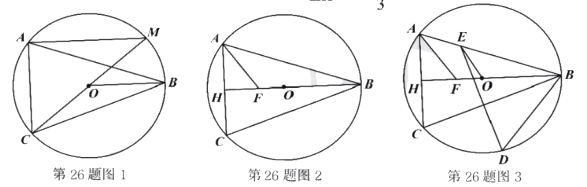
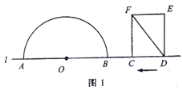
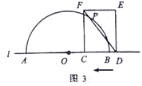
![]() 如图1所示,矩形纸片
如图1所示,矩形纸片![]() 是一张“标准纸”,将纸片折叠一次,使点
是一张“标准纸”,将纸片折叠一次,使点![]() 与
与![]() 重合,再展开,折痕
重合,再展开,折痕![]() 交
交![]() 边于点
边于点![]() 交
交![]() 边于点
边于点![]() ,若
,若![]() 求
求![]() 的长,
的长,
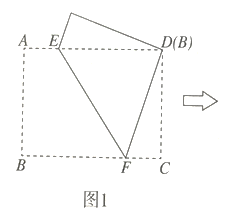
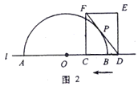
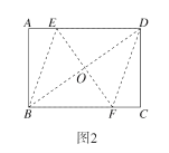
![]() 如图2,在
如图2,在![]() 的基础上,连接
的基础上,连接![]() 折痕
折痕![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 判断四边形
判断四边形![]() 的形状,并说明理由.
的形状,并说明理由.
探究发现:
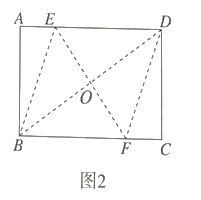
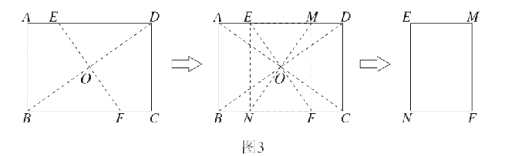
![]() 如图3所示,在(1)和(2)的基础上,展开纸片后,将纸片再折叠一次,使点
如图3所示,在(1)和(2)的基础上,展开纸片后,将纸片再折叠一次,使点![]() 与点
与点![]() 重合,再展开,痕
重合,再展开,痕![]() 交
交![]() 边于点
边于点![]() ,
,![]() 交边于点
交边于点![]() 交
交![]() 也是点
也是点![]() .然后将四边形
.然后将四边形![]() 剪下,探究纸片
剪下,探究纸片![]() 是否为“标准纸”,说明理由.
是否为“标准纸”,说明理由.
【答案】(1) ![]() 长为
长为![]() ;(2) 四边形
;(2) 四边形![]() 是菱形,理由见解析;(3) 纸片
是菱形,理由见解析;(3) 纸片![]() 是“标准纸",理由见解析
是“标准纸",理由见解析
【解析】
(1)![]() ,则
,则![]() ,根据四边形
,根据四边形![]() 是矩形,得到
是矩形,得到![]() ,由折叠得
,由折叠得![]() ,设
,设![]() ,则
,则![]() ,在
,在![]() 中,
中,![]() ,可得
,可得![]() 即可求解.
即可求解.
(2)当顶点![]() 与点
与点![]() 重合时,折痕
重合时,折痕![]() 垂直平分
垂直平分![]() ,可得
,可得![]() ,
,![]() ,在矩形
,在矩形![]() 中,
中,![]() ,得到
,得到![]() ,在
,在![]() 和
和![]() 中,
中,![]() ,可得
,可得![]() ,
,![]() ,再根据
,再根据![]() ,可得四边形
,可得四边形![]() 是平行四边形,最后根据
是平行四边形,最后根据![]() ,即可求证平行四边形
,即可求证平行四边形![]() 是菱形.
是菱形.
(3)由![]() 可知,
可知,![]() ,同理可知,
,同理可知,![]() ,可得四边形
,可得四边形![]() 是平行四边形,根据
是平行四边形,根据![]() ,得到
,得到![]() ,再根据
,再根据![]() ,可得
,可得![]() ,进而得到
,进而得到![]() ,
,![]() ,同理可得,
,同理可得,![]() ,根据四边形
,根据四边形![]() 是矩形,可得
是矩形,可得![]() ,
,![]() ,四边形
,四边形![]() 是矩形,
是矩形,![]() ,
,![]() ,
,![]() ,即可求证纸片
,即可求证纸片![]() 是“标准纸".
是“标准纸".
解:![]() 则
则![]()
![]() 四边形
四边形![]() 是矩形
是矩形
![]()
由折叠得![]()
设![]() ,则
,则![]()
在![]() 中,
中,![]()
![]()
![]()
答:![]() 长为
长为![]()
![]() 四边形
四边形![]() 是菱形.
是菱形.
理由:当顶点![]() 与点
与点![]() 重合时,折痕
重合时,折痕![]() 垂直平分
垂直平分![]()
![]() ,
,![]()
在矩形![]() 中,
中,![]()
![]()
在![]() 和
和![]() 中,
中,![]()
![]()
![]()
![]()
![]() 四边形
四边形![]() 是平行四边形
是平行四边形
![]()
平行四边形![]() 是菱形.
是菱形.
![]() 纸片
纸片![]() 是“标准纸”
是“标准纸”
理由如下:由![]() 可知,
可知,![]()
同理可知,![]()
![]() 四边形
四边形![]() 是平行四边形
是平行四边形
![]()
![]()
![]()
![]()
![]()
![]()
同理可得,![]()
![]() 四边形
四边形![]() 是矩形,
是矩形,
![]() ,
,
![]()
![]() 四边形
四边形![]() 是矩形.
是矩形.
![]() .
.
![]()
![]() .
.
![]() 纸片
纸片![]() 是“标准纸".
是“标准纸".

练习册系列答案
相关题目