题目内容
【题目】如图,△DAC和△EBC均是等边三角形,AE、BD分别与CD、CE交于点M、N,有如下结论:①△ACE≌△DCB;②CM=CN;③AC=DN;④∠DAE=∠DBC.其中正确的有( )

A. ②④ B. ①②③ C. ①②④ D. ①②③④
【答案】C
【解析】∵△DAC和△EBC均是等边三角形,
∴AC=CD,BC=CE,∠ACD=∠BCE=60°,
∴∠ACD+∠DCE=∠BCE+∠DCE,
∴∠ACE=∠BCD,
在△ACE和△BCD中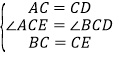 ,
,
∴△ACE≌△DCB(SAS);∴①正确;
∵∠ACD=∠BCE=60°,
∴∠DCE=180°-60°-60°=60°=∠ACD,
∵△ACE≌△DCB,
∴∠NDC=∠CAM,
在△ACM和△DCN中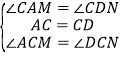 ,
,
∴△ACM≌△DCN(ASA),
∴CM=CN,AM=DN,∴②正确;
∵△ADC是等边三角形,
∴AC=AD,
∠ADC=∠ACD,
∵∠AMC>∠ADC,
∴∠AMC>∠ACD,
∴AC>AM,
即AC>DN,∴③错误;
∵∠DBC+∠CDB=60°,∠DAE+∠EAC=60°,而∠EAC=∠CDB,∴∠DAE=∠DBC,④正确,
∴正确答案①②④,
故选C.

练习册系列答案
相关题目