题目内容
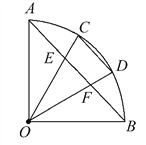
【题目】如图,∠AOB=90°,C,D是![]() 的三等分点,AB分别交OC,OD于点E,F.试找出图中相等的线段(半径除外).
的三等分点,AB分别交OC,OD于点E,F.试找出图中相等的线段(半径除外).
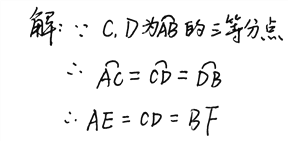
(1)错因: .
(2)纠错:____________________________________________________________
.
【答案】(1) AE,BF不是圆的弦,不能直接利用等弧对等弦(2)10
【解析】试题分析:先根据OA⊥OB可知∠AOB=90°,再由C、D为弧AB的三等分点可求出∠AOC的度数;由三角形内角和定理求出∠OCD的度数,根据三角形外角的性质得出∠OEF及∠OFE的度数,得OE=OF,CE=DF;根据三角形内角和定理即可得出∠AEO的度数;连接AC,BD,可得出CD=AE=BF,可得EF∥CD,所以EF<CD,即可得解.
解:∵在⊙O中,半径OA⊥OB,C、D为弧AB的三等分点,
∴∠AOC=![]() ∠AOB=
∠AOB=![]() ×90°=30°
×90°=30°
∵OA=OB,
∴∠OAB=∠OBA=45°,
∵∠AOC=∠BOD=30°,
∴∠OEF=∠OAB+∠AOC=45°+30°=75°,同理∠OFE=75°,
∴OE=OF,
∴CE=DF;
连接AC,BD,

∵OC=OD,OE=OF,
∴EF∥CD,
∴EF<CD,
∵C,D是弧AB的三等分点,
∴AC=CD=BD,
∵∠AOD,
∴△ACO≌△DCO.
∴∠ACO=∠OCD.
∵∠OEF=∠OAE+∠AOE=45°+30°=75°,∠OCD=![]() =75°,
=75°,
∴∠OEF=∠OCD,
∴CD∥AB,
∴∠AEC=∠OCD,
∴∠ACO=∠AEC.
故AC=AE,
同理,BF=BD.
又∵AC=CD=BD
∴CD=AE=BF.
故答案为:
OE=OF,CE=DF,CD=AE=BF.
点睛: 本题考查的是圆的综合题,涉及到等腰三角形的性质、全等三角形的判定定理等知识.解答本题的关键是求出△ACO≌△DCO,根据全等三角形对应边相等的性质得解.在同圆或等圆中,相等的圆心角或相等的弧所对的弦相等,不要认为所对的线段相等.