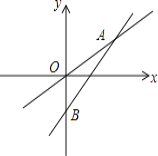
��Ŀ����
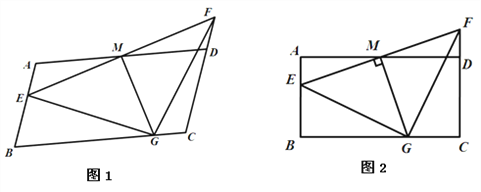
����Ŀ����ͼ����ƽ���ı���ABCD�У�AB��2��AD��4��M��AD���е㣬��E���߶�AB��һ����(�����˶�����A�͵�B)������EM���ӳ����߶�CD���ӳ����ڵ�F��
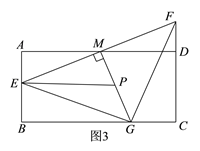
(1) ��ͼ1������֤��AE��DF�� ����EM=3����FEA=45��������M��MG��EF���߶�BC�ڵ�G����ֱ��д����GEF�ĵ���״���������F��AB�ߵľ�����
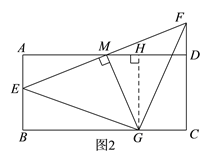
��2���ı�ƽ���ı���ABCD����B�Ķ���������B=90��ʱ���ɵõ�����ABCD����ͼ2�������ж���GEF����״����˵�����ɣ�
��3����(2)�������£�ȡMG�е�P������EP����P���ŵ�E���˶����˶�������E���߶�AB���˶��Ĺ����У���ֱ��д����EPG�����S�ķ�Χ��
���𰸡���1��FH=3![]() �� (2)����ֱ����������֤����������� ��3�� 1��S��2.
�� (2)����ֱ����������֤����������� ��3�� 1��S��2.
�����������������
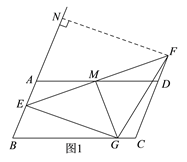
��1��������֪������֤��AME�ա�DMF���Ӷ��ɵ�AE=DF��ME=MF������ME=MF���MG��EF�ڵ�M�ɵ�GE=GF�����ɵõ���GEF�ǵ��������Σ�����F��FN��BA���ӳ����ڵ�N����ϡ�FEA=45���ɵ���FEN�ǵ���ֱ����������������ME�ij������FN�ij��ȣ�
��2������G��GH��AD�ڵ�H�������֪������֤��AME�ա�HGM���Ӷ��ɵ�ME=MG���ɴ˼��ɵõ���MEG=45�㣬��ϣ�1�������ÿ�֪��GEF�ǵ��������Σ��ɴ˿ɵá�GEF��ʱ�ǵ���ֱ�������Σ�
��3������֪�ɵ�S=![]() S��GME������2����֪��GME�ǵ���ֱ�������Σ������Ϊ
S��GME������2����֪��GME�ǵ���ֱ�������Σ������Ϊ![]() ME2�����ɴ˿ɵ�S=
ME2�����ɴ˿ɵ�S=![]() ME2�������Rt��AME����ME�ij�����AE�ij��ȵ�������������S��ȡֵ��Χ��.
ME2�������Rt��AME����ME�ij�����AE�ij��ȵ�������������S��ȡֵ��Χ��.
���������
��1���١���ƽ���ı���ABCD�У�AB��CD��
���EAM=��FDM����AEM=��DFM��
�ߵ�M��AD���е㣬
��AM=DM��
���AME�ա�DMF��
��AE=DF��
������AME�ա�DMF��
��ME=MF��
����MG��EF�ڵ�M��
��MG��EF�Ĵ�ֱƽ���ߣ�
��GE=GF��
���GEF�ǵ�����������
����F��FN��BA���ӳ����ڵ�N�����FNE=90����
�ߡ�AEF=45����EM=3��
���EFN�ǵ���ֱ����������EF=6��
��FN=![]() ������F��AB�ľ���Ϊ
������F��AB�ľ���Ϊ![]() ��
��
��2���ͣ�1��ͬ���ɵá�GEF�ǵ��������Σ�����G��GH��AD�ڵ�H��
�����ı���ABCD�Ǿ��Σ�GM��EF�ڵ�M��
���GHA=��GME=��A=��B=90����
���ı���ABGH�Ǿ��Σ���AME+��GMH=90������HGM+��MGH=90����
��GH=AB=2����AME=��HGM��
����AM=![]() AD=2��
AD=2��
��AM=GH��
����AME�ա�HGM��
��ME=GM��
���MGE�ǵ���ֱ����������
���MEG=45����
����GE=GF��
���FGE=��MEG=45����
���EGF=180��-45��-45��=90����
���GEF�ǵ���ֱ����������
��3����ͼ3���ɣ�2����֪��GEM�ǵ���ֱ�������Σ�
��S��GME=![]() EM2��
EM2��
������P��GM���е㣬
��S=![]() S��GME=
S��GME=![]() EM2=
EM2=![]() EM2��
EM2��
����Rt��AME������AE=0ʱ��ME��С=AM=2����AE=AB=2ʱ��ME���=![]() ��
��
��S��С=![]() EM2=1��S���=
EM2=1��S���=![]() EM2=2��
EM2=2��
��S��ȡֵ��ΧΪ�� ![]() .
.