Question

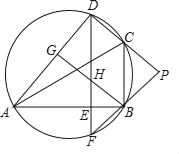
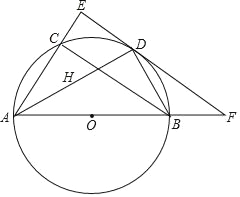
【题目】如图，在直角三角形ABC中，∠ACB＝90°，点H是△ABC的内心，AH的延长线和三角形ABC的外接圆O相交于点D，连结DB．

（1）求证：DH＝DB；

（2）过点D作BC的平行线交AC、AB的延长线分别于点E、F，已知CE＝1，圆O的直径为5．

①求证：EF为圆O的切线；

②求DF的长．

Answer 1

【答案】（1）证明见解析；（2）①证明见解析，②DF＝．

【解析】

（1）先判断出∠DAC=∠DAB，∠ABH=∠CBH，进而判断出∠DHB=∠DBH，即可得出结论；

（2）①先判断出OD∥AC，进而判断出OD⊥EF，即可得出结论；

②先判断出△CDE≌△BDG，得出GB=CE=1，再判断出△DBG∽△ABD，求出DB2=5，即DB=，DG=2，进而求出AE=AG=4，最后判断出△OFD∽△AFE即可得出结论．

（1）证明：连接HB，

∵点H是△ABC的内心，

∴∠DAC＝∠DAB，∠ABH＝∠CBH，

∵∠DBC＝∠DAC，

∴∠DHB＝∠DAB+∠ABH＝∠DAC+∠CBH，

∵∠DBH＝∠DBC+∠CBH，

∴∠DHB＝∠DBH，

∴DH＝DB；

（2）①连接OD，

∵∠DOB＝2∠DAB＝∠BAC

∴OD∥AC，

∵AC⊥BC，BC∥EF，

∴AC⊥EF，

∴OD⊥EF，

∵点D在⊙O上，

∴EF是⊙O的切线；

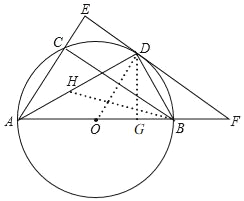
②过点D作DG⊥AB于G，

∵∠EAD＝∠DAB，

∴DE＝DG，

∵DC＝DB，∠CED＝∠DGB＝90°，

∴△CDE≌△BDG，

∴GB＝CE＝1，

在Rt△ADB中，DG⊥AB，

∴∠DAB＝∠BDG，

∵∠DBG＝∠ABD，

∴△DBG∽△ABD，

∴，

∴DB2＝ABBG＝5×1＝5，

∴DB＝，DG＝2，

∴ED＝2，

∵H是内心，

∴AE＝AG＝4，

∵DO∥AE，

∴△OFD∽△AFE，

∴，

∴，

∴DF＝．