Question

【题目】如图，在平面直角坐标系中，将正方形OABC绕点O逆时针旋转45°后得到正方形OA1B1C1 ， 依此方式，绕点O连续旋转2018次得到正方形OA2018B2018C2018 ， 如果点A的坐标为(，0)，那么点B2018的坐标为( )

A. (1，1) B. (0，) C. (﹣1，1) D. (-，0)

Answer 1

【答案】B

【解析】

探寻图形规律的题，根据旋转的方向及性质，分别找出A1,A2,A3,A4,各点的坐标，通过观察发现发现图形旋转8次即可回到起点，由于252×8+2=2018，所以A2016的坐标与A的坐标一样，A2018的坐标就应该与A2一样从而得出答案。

过点A1作A1D⊥OA于点D，

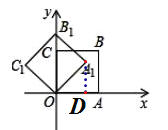
∵A的坐标为(，0)，∴OA=,∵将正方形OABC绕点O逆时针旋转45°后得到正方形OA1B1C1，∴∠AOA1=45°,OA=OA1=,∴OD=A1D,根据勾股定理得：OD=A1D=1，∴A1（1，1），∵将正方形OA1B1C1绕点O逆时针旋转45°后得到正方形OA2B2C2，则A2点落在y轴的正半轴上，∴A2(0,),∵将正方形OA2B2C2绕点O逆时针旋转45°后得到正方形OA3B3C3，则A3点落在第二象限的角平分线上，∴A3(-1，1),∵将正方形OA3B3C3绕点O逆时针旋转45°后得到正方形OA4B4C4，则A4点落在x轴的负半轴上，∴A4(-,0),…

正方形OABC旋转8次则可以回到起点的位置，即A8的坐标与A点的坐标一样（，0），252×8+2=2018，所以A2016的坐标与A的坐标一样，A2018的坐标就应该与A2一样，从而得出A2018的坐标为(0,),

故答案为B.