题目内容
【题目】已知抛物线![]() 的函数解析式为
的函数解析式为![]() ,若抛物线
,若抛物线![]() 经过点
经过点![]() ,对称轴为直线
,对称轴为直线![]() .
.
(1)求抛物线![]() 的解析式.
的解析式.
(2)已知实数![]() ,请证明:
,请证明:![]() ,并说明
,并说明![]() 为何值时才会有
为何值时才会有![]() .
.
(3)若抛物线![]() 先向上平移4个单位,再向左平移1个单位后得到抛物线
先向上平移4个单位,再向左平移1个单位后得到抛物线![]() ,设
,设![]() ,
,![]() 是
是![]() 上的两个不同点,且满足:
上的两个不同点,且满足:![]() ,
,![]() ,
,![]() .请你用含有
.请你用含有![]() 的表达式表示出
的表达式表示出![]() 的面积
的面积![]() ,并求出
,并求出![]() 的最小值及
的最小值及![]() 取最小值时一次函数
取最小值时一次函数![]() 的函数解析式.
的函数解析式.
(参考公式:在平面直角坐标系中,若![]() ,则
,则![]() 两点间的距离
两点间的距离![]() )
)
【答案】(1)![]() ;(2)证明详见解析,当且仅当x=1时,
;(2)证明详见解析,当且仅当x=1时,![]() 成立;(3)
成立;(3)![]()
![]() ,SΔAOB的最小值为1,直线OA的一次函数解析式为y=x
,SΔAOB的最小值为1,直线OA的一次函数解析式为y=x
【解析】
(1)直接利用待定系数法求出解析式即可;
(2)利用平方的非负数可知:![]() ,移项即可解答;
,移项即可解答;
(3)根据平移规则得到![]() 的解析式:
的解析式:![]() . 则A(m,m2),B(n,n2),利用勾股定理列式求得:
. 则A(m,m2),B(n,n2),利用勾股定理列式求得:![]() ,代入面积公式得到SΔAOB=
,代入面积公式得到SΔAOB=![]() =
=![]() =
=![]() ,再利用(2)中结论即可得出结论.
,再利用(2)中结论即可得出结论.
(1)∵ 抛物线![]() 过点
过点![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∴![]() .
.
又∵ 抛物线![]() 的对称轴为直线
的对称轴为直线![]()
∴ ![]() ,即
,即![]() .
.
∴ 抛物线![]() 的解析式为
的解析式为![]() .
.
(2) ∵![]() ,∴
,∴![]() ,
,
∴![]() ,当且仅当x=1时,
,当且仅当x=1时,![]() 成立.
成立.
(3)由(1)知抛物线![]() 解析式为
解析式为![]() ,
,
抛物线![]() 是抛物线
是抛物线![]() 先向上平移4个单位,再向左平移1个单位后得到的,
先向上平移4个单位,再向左平移1个单位后得到的,
∴ 抛物线![]() 的解析式为
的解析式为![]() .
.
∵![]() ,
,![]() 是
是![]() 上的两个不同点,
上的两个不同点,
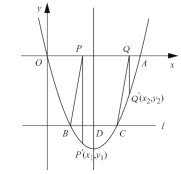
∴A(m,m2),B(n,n2).
又∵![]() ,
,![]() ,
,![]() ,
,
∴ OA2+OB2=AB2,
∴ m2+m4+n2+n4=(m-n)2+(m2-n2)2,
化简得:![]() .
.
∵ SΔAOB=![]() =
=![]()
![]() .
.
由(2)知:当且仅当![]() 时,上式等号成立.
时,上式等号成立.
又∵![]() ,
,![]() ,且
,且![]() ,
,
∴![]() ,
,![]() ,
,
∴ SΔAOB的最小值为1,此时m=1,A(1,1),
∴ 直线OA的一次函数解析式为y=x.

 名校课堂系列答案
名校课堂系列答案【题目】在创客教育理念的指引下,国内很多学校都纷纷建立创客实践及创客空间,致力于从小培养学生的创新精神和创造能力,某校开设了“3D”打印,数学编程,智能机器人,陶艺制作,这四门创客课程,为了了解学生对这四门创客课程的喜爱情况,数学兴趣小组对全校学生进行了随机问卷调查,将调查结果整理后绘制成如下的统计图表:
创客课程 | 频数 | 频率 |
“3D”打印 | 36 | 0.45 |
数学编程 | 0.25 | |
智能机器人 | 16 | b |
陶艺制作 | 8 | |
合计 | a | 1 |

根据图表中提供的信息回答下列问题:
(1)统计表中的a=________,b=________;
(2)“陶艺制作”对应扇形的圆心角度数为________;
(3)若该校有学生2000人,请估算全校喜爱“智能机器人”的人数有多少?