题目内容
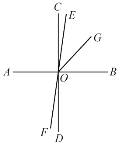
【题目】如图，直线AB、CD、EF都经过点O，且AB⊥CD，OG平分∠BOE，如果∠EOG＝
∠AOE，求∠EOG，∠DOF和∠AOE.
【答案】40°，10°，10°.
【解析】直线AB，CD，EF都经过点O，且AB⊥CD，OG平分∠BOE，根据对顶角相等以及角平分线的性质，转化相等关系，然后根据已知条件求出∠EOG，∠DOF和∠AOE的度数．
∵OG平分∠BOE，∴∠BOE＝2∠EOG，
又∵∠EOG＝
∠AOE，∴∠AOE＝
∠EOG，
∵∠AOE＋∠BOE＝180°，∴∠EOG＋2∠EOG＝180°，即
∠EOG＝180°，
∴∠EOG＝40°，
∴∠AOE＝∠EOG＝×40°＝100°，∠BOE＝2∠EOG＝2×40°＝80°，
∵AB⊥CD，∴∠BOC＝90°，
∴∠EOC＝∠BOC－∠BOE＝90°－80°＝10°，
∴∠DOF＝∠EOC＝10°.
本题考查了角的计算、对顶角、邻补角、垂线等知识，根据邻补角互补以及角平分线的性质，转化相等关系是解题的关键.
练习册系列答案
相关题目
