题目内容
【题目】如图,长方形ABCD中,AD=BC=6,AB=CD=4.点P从点A出发,以每秒1个单位的速度沿A→B→C→D→A的方向运动,回到点A停止运动.设运动时间为t秒.
(1)当t= 时,点P到达点C;当t= 时,点P回到点A;
(2)△ABP面积取最大值时t的取值范围;(3)当△ABP的面积为3时,求t的值;
(4)若点P出发时,点Q从点A出发,以每秒2个单位的速度沿A→D→C→B→A的方向运动,回到点A停止运动.请问:P 、Q何时在长方形ABCD的边上相距1个单位长度?

【答案】(1)当t=10,点p到点C,当t=20,点p到点A;(2)10≤t≤14;(3)t=5.5或t=18.5; (4)t=![]() 或 t=7.
或 t=7.
【解析】
(1)根据长方形ABCD的边长和点P的运动速度进行计算即可;
(2)由图可知,当点P在边CD上运动时,△ABP的面积最大,由此根据已知条件计算出点P在边CD上运动所对应的时间范围即可;
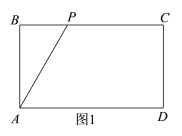
(3)如图1和图2,分点P在BC上和AD上两种情况结合已知条件解答即可;
(4)由题意可知,点P、Q在长方形ABCD上从A点出发,作相向运动,因此存在以下两种情况: ①点P、Q相遇前相距1个单位长度,如下图3所示;②点P、Q相遇后相距1个单位长度,如下图4所示;结合已知条件分这两种情况解答即可.
(1)∵AD=BC=6,AB=CD=4,
∴AB+BC=10,AB+BC+CD+DA=20,
又∵点P的移动速度为每秒1个单位长度,
∴点P由A到C所需时间为:10÷1=10(秒),
点P由A出发回到A所需时间为:20÷1=20(秒);
(2)由图可知,当点P在边CD上运动时,△ABP的面积最大,
∵AB+BC+CD=14,
∴点P移动到点D的时间为:14÷1=14(秒),
又∵点P移动到点C的时间为10秒,
∴当△ABP的面积最大时,![]() ;
;
(3)①如图1,当点P在边BC上时,由已知可得:AB=4,PB=(t-4),由题意可得:
S△ABP=![]() ,解得:
,解得:![]() ;
;
②如图2,当点P在边AD上时,由已知可得:AB=4,AP=(20-t),由题意可得:S△ABP=![]() ,解得:
,解得:![]() ,
,
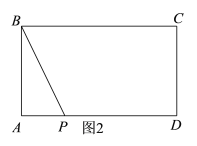
综上所述,当t=5.5或t=18.5时,△ABP的面积为3.
(4)①如图3,当点P、Q相遇前相距1个单位长度时,
由题意可得:![]() ,解得:
,解得:![]() ;
;

②如图4,当点P、Q在相遇后相距1个单位长度时,由题意可得:
![]() ,解得:
,解得:![]() ,
,

综上所述,当![]() 或
或![]() 时,点P、Q在长方形ABCD的边上相距1个单位长度.
时,点P、Q在长方形ABCD的边上相距1个单位长度.

 阅读快车系列答案
阅读快车系列答案【题目】体育课上,全班男同学进行了100米测验,达标成绩为15秒,如表是某小组8名男生的成绩记录,其中“![]() “表示成绩大于15秒.
“表示成绩大于15秒.
|
|
|
|
|
|
|
|
问:![]() 这个小组男生最优秀的成绩是多少秒?最差的成绩是多少秒?
这个小组男生最优秀的成绩是多少秒?最差的成绩是多少秒?
![]() 这个小组男生的达标率为多少?
这个小组男生的达标率为多少?![]() 达标率
达标率![]()
![]() 这个小组男生的平均成绩是多少秒?
这个小组男生的平均成绩是多少秒?